Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bai 1:
\(\omega=\sqrt{\dfrac{k}{m}}\Rightarrow m=\dfrac{k}{\omega^2};v=x'=-\omega A\sin\left(\omega t+\varphi\right)\)
\(W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}\dfrac{k}{\omega^2}.\omega^2A^2.\sin^2\left(\omega t+\varphi\right)=\dfrac{1}{4}kA^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_d=\dfrac{1}{4}.\omega^2.m.A^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]=\dfrac{1}{4}.100.0,2.4\left[1-\cos\left(20t\right)\right]=20\left[1-\cos\left(20t\right)\right]\)
Bai 2:
\(W_t=\dfrac{1}{2}kx^2=m\omega^2A^2.\dfrac{\cos\left(2\omega t+\varphi\right)+1}{4}=\dfrac{1}{4}m\omega^2.A^2\left[1+\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_t=\dfrac{1}{4}.0,1.100.36.\left[1+\cos\left(2.10t\right)\right]=90.\left[1+\cos20t\right]\)

\(\omega=\sqrt{\frac{k}{m}}\Leftrightarrow10=\sqrt{\frac{k}{0,1}}\Rightarrow k=10\)N/m
\(W_t=\frac{1}{2}kx^2=\frac{1}{2}.10.2^2=20J\)
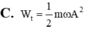
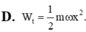

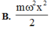
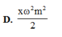
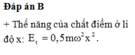

a/ Ủa câu 1 ko nói rõ là tính thế năng ở vị trí nào ạ? Vậy em tính tại VTCB nhé :v
Tại vị trí cân bằng thì động năng lớn nhất, do li độ của vật bằng 0
\(W_t=W_d=\frac{1}{2}mv_{max}^2\)
\(v_{max}=\omega A\Rightarrow W_t=\frac{1}{2}m\omega^2A^2=...\)
2/ Thế năng biến thiên tuần hoàn heo thời gian với tần số là \(2f\)\(\Rightarrow2f=2.\frac{\omega}{2\pi}=\frac{2\pi f}{\pi}=f\Rightarrow B\)
3/ Động năng biến thiên tuần hoàn theo thời gian với tần số góc là \(2\omega\)
=> C