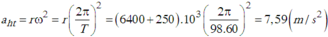Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đúng vì cơ năng bằng tổng của thế năng và cơ năng khi viên đạn bay thì cả 2 đều dương nên cơ năng dương

Câu 28: Vệ tinh địa tĩnh là vệ tinh nhân tạo của Trái Đất, quay xung quanh Trái Đất với chu kì bằng chu kì tự quay của Trái Đất là 24 giờ, sao cho vệ tinh này dường như luôn đứng yên đối với một điểm ở mặt đất. Một vệ tinh địa tĩnh chuyển động trên quỹ đạo bán kính r, tốc độ dài là 3071(m/s). Bán kính quĩ đạo tròn và gia tốc hướng tâm của vệ tinh là.
A. r=4,22.10^7m;a=0,22m/s^2
B. r=8,22.10^7m;a=0,22m/s^2
C. r=4,22.10^7m;a=0,434m/s^2
D. r=8,22.10^7m;a==0,434m/s^2
Bài giải:
Chu kì: \(T=24h=24\cdot3600=86400s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{86400}\approx7,27\cdot10^{-5}\)(rad/s)
Tốc độ dài: \(v=3071\)m/s
Bán kính quỹ đạo tròn: \(R=\dfrac{v}{\omega}=\dfrac{3071}{7,27\cdot10^{-5}}=4,22\cdot10^7m\)
Gia tốc hướng tâm: \(a_{ht}=\dfrac{v^2}{R}=\dfrac{3071^2}{\left(4,22\cdot10^7\right)}\approx0,22\)m/s2
Chọn A.

\(a_{ht}=g=\frac{v^2}{R}=\frac{v^2}{\left(6400+200\right).1000}=9,2\)
=> v=?

Tốc độ góc và gia tốc hướng tâm của vệ tinh được tính theo các công thức
ω = 2 π /T = (2.3.14)/(88.60) ≈ 1.19. 10 - 3 (rad/s)
a h t = ω 2 (R + h) = 1 . 19 . 10 - 3 2 .6650. 10 3 = 9,42 m/ s 2

a.
Ta có:
\(v=\sqrt{\dfrac{g_0\cdot R^2}{R+h}}=\sqrt{\dfrac{9,8+\left(6400\cdot1000\right)^2}{6400\cdot1000+25630\cdot1000}}=3540,1\left(\dfrac{m}{s}\right)\)
Tốc độ góc:
\(\omega=\dfrac{v}{R}=\dfrac{3540,1}{6400\cdot1000}=5,5\cdot10^{-4}\left(\dfrac{rad}{s}\right)\)
b.
\(a_{ht}=\dfrac{v^2}{R}=\dfrac{3540,1^2}{6400\cdot1000}\approx2\left(\dfrac{m}{s^2}\right)\)
Không có tốc độ hướng tâm, chỉ có gia tốc hướng tâm bạn nhé

a. Chuyển động của vệ tinh có gia tốc. Vì vệ tinh chuyển động động tròn đều nên có gia tốc là gia tốc hướng tâm.
b. \(t=24h=86400s\)
\(\Rightarrow\omega=\dfrac{2\pi}{t}=\dfrac{\pi}{43200}\)rad/s
\(R'=0,5R=3200km=32.10^5m\)
Khi đó \(v=\omega R'=\dfrac{\pi}{43200}32.10^5=74.07\pi\)(m/s)
Vậy: \(v=74,07\pi\)(m/s)

a. Ta có: \(8km/s=8000m/s\)
Khoảng cách từ vệ tinh đến trái đất:
\(r=\left(600.10^3\right)+\left(6400.10^3\right)=7.10^6m\)
Tốc độ góc của vệ tinh bạy 1 vòng trái đất:
\(\omega=\dfrac{v}{r}=\dfrac{8000}{7.10^6}=\dfrac{1}{875}\left(rad/s\right)\)
b. Chu kì của vệ tinh bay hết một vòng trái đất:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2.3,14}{\dfrac{1}{875}}=5495s\)