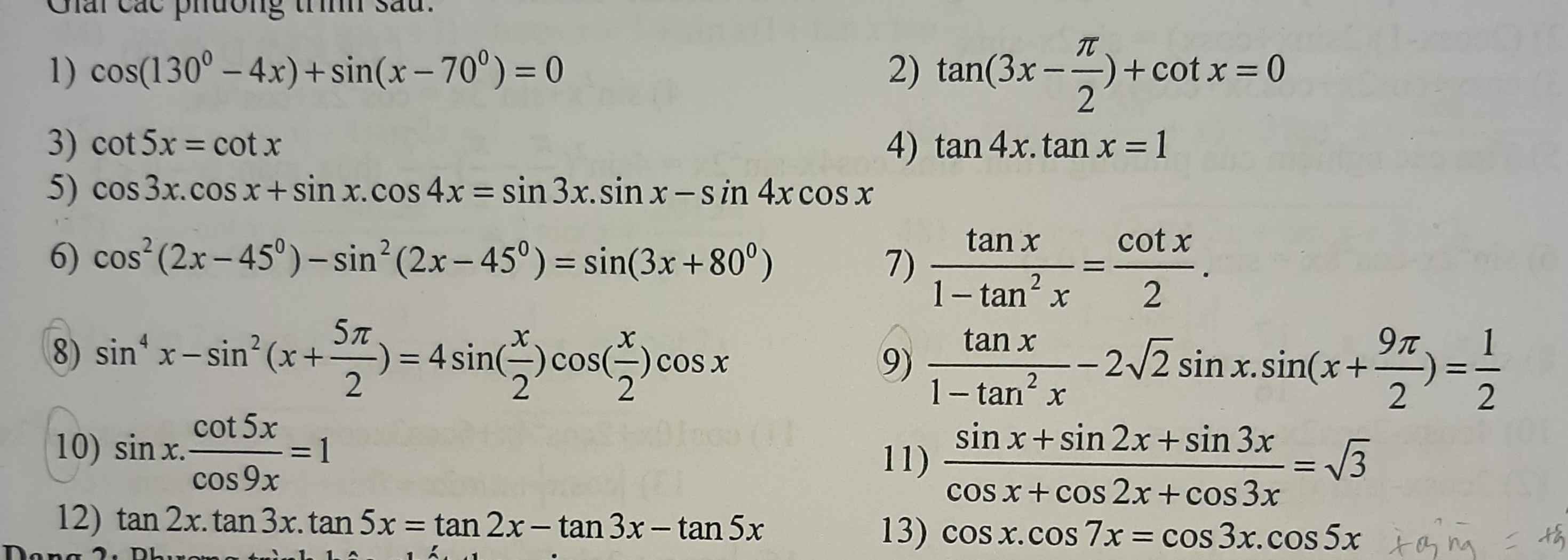PM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
R
3
14 tháng 5 2022
Bài 2:
a: \(=\dfrac{7}{9}\left(\dfrac{7}{6}-\dfrac{19}{20}-\dfrac{1}{15}\right)+\dfrac{22}{5}\cdot\dfrac{1}{24}\)
\(=\dfrac{7}{9}\cdot\dfrac{3}{20}+\dfrac{22}{120}=\dfrac{7}{60}+\dfrac{11}{60}=\dfrac{18}{60}=\dfrac{3}{10}\)
b: \(=\left(\dfrac{35-32}{60}\right)^2+\dfrac{4}{5}\cdot\dfrac{70-45}{80}\)
\(=\dfrac{1}{400}+\dfrac{4\cdot25}{400}=\dfrac{101}{400}\)
25 tháng 6 2017
a) \(100+98+96+...+2-97-95-93-...-3\)
= \(100+98+\left(96-97\right)+\left(94-95\right)+...+\left(2-3\right)\)
= \(100+98-95\) = \(103\)
b) \(2-4-6+8+10-12-14+16+...-102+104\)
= \(\left(2-4\right)+\left(-6+8\right)+\left(10-12\right)+\left(-14+16\right)+...+\left(-102+104\right)\)
= \(-2+2-2+2-2+...+2\) = \(0\)
c) \(1+2-3-4+5+6-7-8+9+10-11-12+...-111-112+113+114\)
= \(\left(1+2\right)-\left(3+4\right)+\left(5+6\right)-\left(7+8\right)+...\left(113+114\right)\)
= \(3-7+11-15+19-23+...+219-223+227\)
= \(\left(3-7\right)+\left(11-15\right)+\left(19-23\right)+...+\left(219-223\right)+227\)
= \(-4-4-4-4-...-4+227\)
= \(54\left(-4\right)+227\) = \(-216+227\) = \(11\)
AN
6
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 6 2021
8.
\(\Leftrightarrow sin^4x-cos^2x=2sinx.cosx\)
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^4x\) ta được:
\(tan^4x-\dfrac{1}{cos^2x}=2tanx.\dfrac{1}{cos^2x}\)
\(\Leftrightarrow tan^4x-\left(1+tan^2x\right)=2tanx\left(1+tan^2x\right)\)
\(\Leftrightarrow tan^4x-2tan^3x-tan^2x-2tanx-1=0\)
Wel well, đề bài sai, phương trình bậc 4 này không giải được
PT
26 tháng 6 2017
Hờ, bài toán này mà mình cứ ngồi tính tổng như thật -,-
\(\text{1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + 10 - 11 - 12 + ... - 111 - 112 + 113 + 114}\)\(=1+\left(2-3-4+5\right)+\left(6-7-8+9\right)+\left(10-11-12+13\right)+...+\left(110-111-112+113\right)+114\)\(=1+114=115\)
26 tháng 6 2017
Lớp 5: chương trình nâng cao nhé các bạn! ko có số âm nhé!
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2020
Bài 4:
\(u_n=5.\left(\frac{1}{2}\right)^{2n-1}=10.\left(\frac{1}{2}\right)^{2n}=10\left(\frac{1}{4}\right)^n\)
Là cấp số nhân với \(u_1=10\) và công bội \(q=\frac{1}{4}\)
Bài 5:
\(S_5=u_1.\frac{q^4-1}{q-1}=u_1.\frac{\left(\frac{1}{3}\right)^4-1}{\frac{1}{3}-1}=\frac{121}{81}u_1\)
\(\Rightarrow u_1=\frac{81}{121}S_5=81\)
Bài 6:
\(\left\{{}\begin{matrix}u_1q=4\\u_1q^3=9\end{matrix}\right.\) \(\Rightarrow\left(u_1q^2\right)^2=36\Rightarrow\left[{}\begin{matrix}u_1q^2=6\\u_1q^2=-6\end{matrix}\right.\)
Mà \(u_3=u_1q^2\Rightarrow u_3=\pm6\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2020
Bài 2:
\(\left\{{}\begin{matrix}u_1q^3-u_1q=24\\u_1q^2-u_1=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1q\left(q^2-1\right)=24\\u_1\left(q^2-1\right)=12\end{matrix}\right.\)
\(\Leftrightarrow\frac{u_1q\left(q^2-1\right)}{u_1\left(q^2-1\right)}=\frac{24}{12}\Rightarrow q=2\Rightarrow u_1=\frac{12}{q^2-1}=4\)
\(\Rightarrow S_8=u_1.\frac{q^8-1}{q-1}=4\left(2^8-1\right)=...\)
Câu 3:
\(u_{10}=u_1q^9=4\left(-2\right)^9=-2^{11}\)
\(S_{15}=u_1.\frac{q^{15}-1}{q-1}=4.\frac{\left(-2\right)^{15}-1}{-3}=\frac{3}{4}\left(2^{15}+1\right)\)
