K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 2 2022
Bài 3:
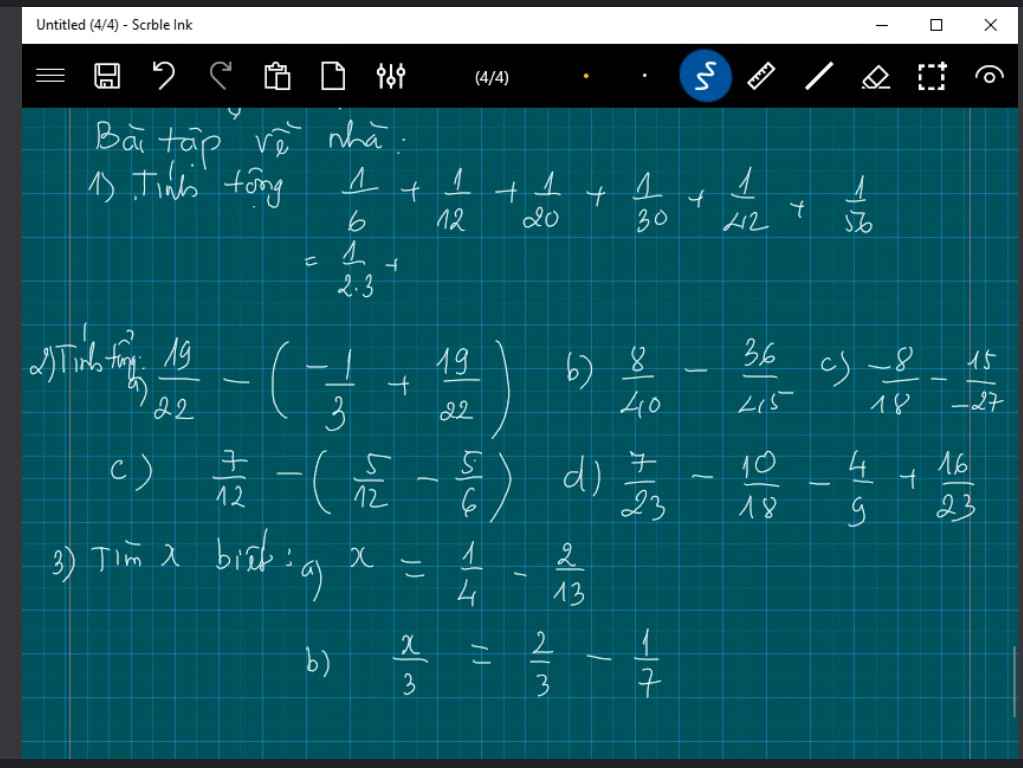
a: \(x=\dfrac{1}{4}-\dfrac{2}{13}=\dfrac{13}{52}-\dfrac{8}{52}=\dfrac{5}{52}\)
b: \(\dfrac{x}{3}=\dfrac{2}{3}-\dfrac{1}{7}\)
nên \(x\cdot\dfrac{1}{3}=\dfrac{14}{21}-\dfrac{3}{21}=\dfrac{11}{21}\)
hay \(x=\dfrac{11}{21}:\dfrac{1}{3}=\dfrac{11}{7}\)
HY
3
23 tháng 4 2020
- 12 + 3(-x + 7) = -12 -3x - 21 = -3x - 33 = -3(x + 11)
H9
HT.Phong (9A5)
CTVHS
8 tháng 8 2023
\(\left(2x-15\right)^5=\left(2x-15\right)^3\)
\(\Rightarrow\left(2x-15\right)^5-\left(2x-15\right)^3=0\)
\(\Rightarrow\left(2x-15\right)^3\left[\left(2x-15\right)^2-1\right]=0\)
\(\Rightarrow\left(2x-15\right)^3\left(2x-15-1\right)\left(2x-15+1\right)=0\)
\(\Rightarrow\left(2x-15\right)^3\left(2x-16\right)\left(2x-14\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-15=0\\2x-16=0\\2x-14=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=15\\2x=16\\2x=14\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}\\x=8\\x=7\end{matrix}\right.\)
NT
1
9 tháng 7 2023
A=1/2^2+1/3^2+...+1/10^2
=>A<1-1/2+1/2-1/3+...+1/9-1/10=1-1/10<1
NP
2
16 tháng 9 2017
S = 1.3 + 2.4 + 3.5 + 4.6 + ..... + 99.101 + 100.102
= 1.(2 + 1) + 2(3 + 1) + 3.(4 + 1) + ......... + 99(100 + 1) + 100.(101 + 1)
= 1.2 + 1 + 2.3 + 1 + 3.4 + 3 + ........ + 99.100 + 99 + 100.101 + 100
= (1.2 + 2.3 + 3.4 + ....... + 100.101 ) + (1 + 2 + 3 + ....... + 100)
Ta có công thức :
1.2+2.3+3.4+....+n(n+1)=n(n+1)(n+2)/3
1+2+3+...+n=n(n+1)/2
Áp dụng vào bài toán ta được :
S=100.101.102/3 +100.101/2
= 343400 + 5050
= 348450
PT
3
19 tháng 2 2022
a: =-5/6-3/7=-35/42-18/42=-53/42
b: =2/5-4/9=18/45-20/45=-2/45
c: =-24/35
d: =2/3x-5/4=-10/12=-5/6
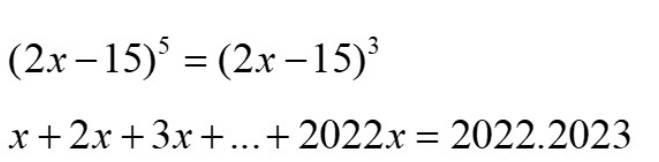
\((-12).36 - 12.64 =-432 - 768 =-1200\)