K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PV
4
20 tháng 9 2020
Bạn ơi cho mình hỏi từ sau chỗ \(\frac{1}{2004.2003}\)là dấu trừ hết ạ? Nếu là dấu cộng thì mình làm được :33
CT
3
29 tháng 8 2015
A = 7/7.17 + 7/17.27 + 7/27.37 + ............ +7/1997.2007
A=7/10 ( 10/7.17 + 10/17.27 + 10/27.37 + ................+10/1997.2007)
A= 7/10 ( 1/7 -1/17 + 1/17 - 1/27 + 1/27 - 1/37 +...............+ 1/1997 - 1/2007)
A= 7/10 (1/7 - 1/2007)
A= 7/10 . 2000/14049
A=200/2007
bây h mk có vc rùi tích đúng nha tối mk lm típ cho
DK
1
11 tháng 9 2021
\(\dfrac{1}{2014}-\dfrac{1}{2014.2013}-\dfrac{1}{2013.2012}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}=\dfrac{1}{2014}-\left(\dfrac{1}{2013.2014}+\dfrac{1}{2012.2013}+...+\dfrac{1}{2.3}+\dfrac{1}{1.2}\right)=\dfrac{1}{2014}-\left(\dfrac{1}{2013}-\dfrac{1}{2014}+\dfrac{1}{2012}-\dfrac{1}{2013}+...+\dfrac{1}{2}-\dfrac{1}{3}+1-\dfrac{1}{2}\right)=\dfrac{1}{2014}-\left(1-\dfrac{1}{2014}\right)=\dfrac{1}{2014}-\dfrac{2013}{2014}=-\dfrac{1006}{1007}\)
DS
1
1 tháng 7 2023
=1/2014-(1/1*2+1/2*3+...+1/2013*2014)
=1/2014-(1-1/2+1/2-1/3+...+1/2013-1/2014)
=1/2014-1+1/2014
=1/1007-1=-1006/1007
HL
14 tháng 7 2017
\(\dfrac{1}{2003.2002}-\dfrac{1}{2002.2001}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
= \(\dfrac{1}{2003.2002}-\left(\dfrac{1}{2002.2001}+...+\dfrac{1}{3.2}+\dfrac{1}{2.1}\right)\)
= \(\dfrac{1}{2003.2002}-\left(\dfrac{1}{2002}-\dfrac{1}{2001}+...+\dfrac{1}{3}-\dfrac{1}{2}+\dfrac{1}{2}-1\right)\)
= \(\dfrac{1}{2003.2002}-\dfrac{1}{2002}+1\)
= \(\dfrac{1-2003+2003.2002}{2003.2002}\)
= \(1-\dfrac{2002}{2003.2002}=1-\dfrac{1}{2003}\) = \(\dfrac{2002}{2003}\)
26 tháng 6 2017
a) \(\frac{1}{99}-\frac{1}{99.98}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(=\frac{1}{99}-\left(\frac{1}{99.98}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
đặt \(A=\frac{1}{99.98}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(A=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{98.99}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{98}-\frac{1}{99}\)
\(A=1-\frac{1}{99}\)
\(A=\frac{98}{99}\)
thay A vào, ta được :
\(\frac{1}{99}-\frac{98}{99}=\frac{-97}{99}\)
b) \(\frac{2}{100.99}-\frac{2}{99.98}-...-\frac{2}{3.2}-\frac{2}{2.1}\)
\(=\frac{2}{100.99}-\left(\frac{2}{99.98}+...+\frac{2}{3.2}+\frac{2}{2.1}\right)\)
đặt \(A=\frac{2}{99.98}+...+\frac{2}{3.2}+\frac{2}{2.1}\)
\(A=\frac{2}{1.2}+\frac{2}{2.3}+...+\frac{2}{98.99}\)
\(A=2.\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{98.99}\right)\)
\(A=2.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{98}-\frac{1}{99}\right)\)
\(A=2.\left(1-\frac{1}{99}\right)\)
\(A=2.\frac{98}{99}\)
\(A=\frac{196}{99}\)
Thay A vào, ta được :
\(\frac{2}{100.99}-\frac{196}{99}=\frac{-19598}{9900}\)
S
1
5 tháng 11 2021
\(=\dfrac{1}{100}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{100}-\dfrac{99}{100}=-\dfrac{49}{50}\)
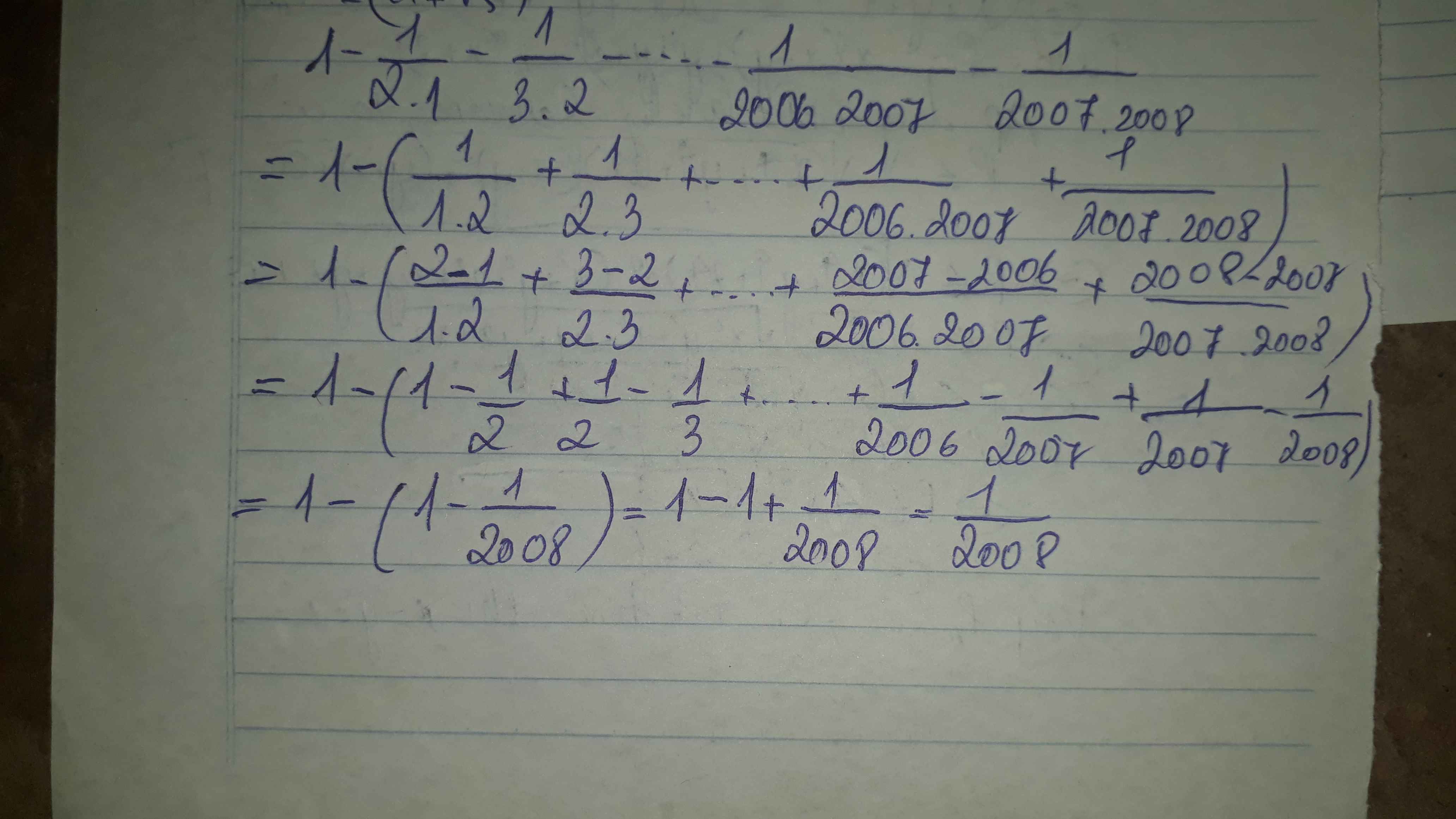
Ta có : \(\dfrac{1}{2006.2005}+....+\dfrac{1}{3.2}+\dfrac{1}{2.1}\)
\(=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2005.2006}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{2005}-\dfrac{1}{2006}\)
\(=1-\dfrac{1}{2006}=\dfrac{2005}{2006}\)