
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3


Toán 12 đây chắc vội thế cơ à?
Em giúp cho
Câu hỏi của Kaitou Kid - Toán lớp 9 - Học toán với OnlineMath
áp án:
Với 3 số 3, cách làm rất đơn giản: 3 x 3 - 3 = 6.
Sử dụng phép 6 + 6 - 6 = 6 đối với 3 số 6.
Đối với 3 số 4, ta có thể sử dụng phép căn bậc hai từng số rồi tính tổng của chúng.
Với 3 số 9, ta sử dụng phép căn bậc hai của 9 thành 3 rồi tính như trong trường hợp 3 số 3.
Cách làm đối với 3 số 5 và 3 số 7 tương tự nhau:
5 + 5 : 5 = 6
7 - 7 : 7 = 6
3 số 8 là trường hợp dễ gây nhầm lẫn nhất vì nhiều người sẽ sử dụng phép căn bậc ba của 8 bằng 2 rồi tính tổng của chúng. Tuy nhiên, người ra đề quy định, người giải không được thêm bất kỳ số tự nhiên nào trong khi ký hiệu căn bậc ba có số 3.
Trong trường hợp này, Ty Yann dùng hai lần căn bậc hai của 8 + 8 (tương đương căn bậc 4 của 16) bằng 2. Sau đó, ông dùng phép tính 8 - 2 = 6.
Với 3 số 1, tác giả dùng phép giai thừa:
(1 + 1 + 1)! = 3! = 3 x 2 x 1 = 6.

Các con số 3, 6, 9 gắn liền với cuộc đời của thiên tài Nikola Tesla vì ông cho rằng chúng là chìa khóa giải mã bí mật vũ trụ. ... Tất cả các thiết kế của ông - khoảng 300 trong số đó được cấp bằng sáng chế - đều hướng tới tương lai và đó là lý do mọi người gọi ông là "nhà phát minh ra thế kỷ 20".
đây là mình tham khảo mạng nhé, chứ bn có bổ sung thì bn tự bổ sung nha

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

Đó là số 2 nha mọi người! giải thích:
( vì câu hỏi là số mấy nên sẽ chú ý vào các số )
-Có hai cây cầu: cầu 1 và cầu 2
-Có từ 1 con trở lên
1> {1,2}
Vậy cần số nào đó lớn hơn 1 trong hai số trên.Suy ra...Số hai là số phừ hợp với điều kiện trên

Khó quá à mọi người!
Đáp án nè: Đó là số 2. Giải thích:
Vì câu hỏi ở đây là số mấy nên sẽ chú ý vào các chữ số.
-Có hai cây cầu là : cầu thứ nhất và cầu thứ hai
-Trong vườn thú các động vật đều trên 1 con
Vậy ta có:{1,2} và biết rằng trên 1
1> {1,2}
Vậy số 2 đủ thỏa mãn điều kiện trên.

Không gian mẫu: \(C_{17}^5\)
a. Số cách chọn sao cho có đúng 3 nam (nghĩa là chọn 3 nam từ 9 nam và 2 nữ từ 8 nữ):
\(n_A=C_9^3.C_8^2\)
Xác suất: \(P_A=\dfrac{C_9^3.C_8^2}{C_{17}^5}=...\)
b. Chọn nhiều nhất 1 nữ nghĩa là ta có 2 TH có thể xảy ra: có 1 nữ và 4 nam hoặc cả 5 đều nam
Số cách chọn: \(n_B=C_8^1.C_4^9+C_9^5\)
Xác suất: \(P_B=\dfrac{C_8^1.C_9^4+C_9^5}{C_{17}^5}=...\)
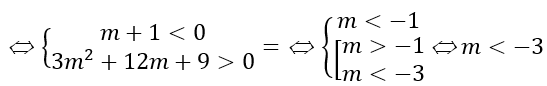
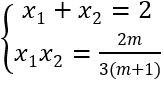
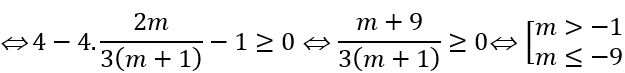
1 + 1 = 2 nha!
Bằng 2