Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Δ=(-3)^2-4(m-2)
=9-4m+8
=17-4m
Đểphương trình có 2 nghiệm phân biệt thì -4m+17>0
=>-4m>-17
=>m<17/4
b: TH1: m=5
=>-x+1=0
=>x=1(loại)
TH2: m<>5
Δ=(-1)^2-4(m-5)
=1-4m+20=21-4m
Để phương trình có hai nghiệm phân biệt thì 21-4m>0
=>4m<21
=>m<21/4
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .
\(x^2-2\left(2m+1\right)x+4m^2+4m=0\)
Để pt có hai ng pb\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow4>0\left(lđ\right)\)
\(\Rightarrow\)Pt luôn có hai ng pb với mọi m
\(\left\{{}\begin{matrix}x_1=\dfrac{2\left(2m+1\right)+\sqrt{4}}{2}=2m+2\\x_2=\dfrac{2\left(2m+1\right)-\sqrt{4}}{2}=2m\end{matrix}\right.\)
Có \(\left|x_1-x_2\right|=x_1+x_2\)
\(\Leftrightarrow\left|2m+2-2m\right|=2m+2+2m\)
\(\Leftrightarrow2=4m+2\)
\(\Leftrightarrow m=0\)
Vậy...
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >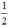 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =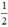 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <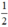 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <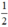 
; có nghiệm kép khi m = 
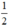và vô nghiệm khi m >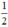 
a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >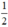 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =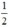 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <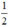 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <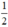 
; có nghiệm kép khi m = 
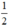và vô nghiệm khi m >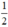 
2.giải phương trình trên , ta được :
\(x_1=\frac{-m+\sqrt{m^2+4}}{2};x_2=\frac{-m-\sqrt{m^2+4}}{2}\)
Ta thấy x1 > x2 nên cần tìm m để x1 \(\ge\)2
Ta có : \(\frac{-m+\sqrt{m^2+4}}{2}\ge2\) \(\Leftrightarrow\sqrt{m^2+4}\ge m+4\)( 1 )
Nếu \(m\le-4\)thì ( 1 ) có VT > 0, VP < 0 nên ( 1 ) đúng
Nếu m > -4 thì ( 1 ) \(\Leftrightarrow m^2+4\ge m^2+8m+16\Leftrightarrow m\le\frac{-3}{2}\)
Ta được : \(-4< m\le\frac{-3}{2}\)
Tóm lại, giá trị phải tìm của m là \(m\le\frac{-3}{2}\)
=>(x1-1)[x2^2-x2(x1+x2-1)+x1x2+1]=-3
=>(x1-1)[-x1x2+x2+x1x2+1]=-3
=>(x1-1)(x2+1)=-3
=>x1x2+(x1-x2)-1=-3
=>(x1-x2)=-3+1-x1x2=-2-m+5=-m+3
=>(x1+x2)^2-4x1x2=m^2-6m+9
=>4^2-4(m-5)=m^2-6m+9
=>4m-20=16-m^2+6m-9=-m^2+6m+7
=>4m-20+m^2-6m-7=0
=>m^2-2m-27=0
=>\(m=1\pm2\sqrt{7}\)
Để pt có hai nghiệm pb:
\(\Leftrightarrow\)\(\Delta=16-4\left(m-4\right)>0\)\(\Leftrightarrow8>m\)
Có\(\left(x_1-1\right)\left(x_2^2-3x_2+m-3\right)=-2\)
\(\Leftrightarrow\left(x_1-1\right)\left(x^2_2-4x_2+m-4\right)+\left(x_1-1\right)\left(x_2+1\right)=-2\)
\(\Leftrightarrow x_1x_2+x_1-x_2-1=-2\) (*) (vì x2 là một nghiệm của pt nên \(x_2^2-4x_2+m-4=0\))
TH1: \(x_1>x_2\)
(*)\(\Leftrightarrow x_1x_2+\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}+1=0\)
\(\Leftrightarrow m-4+\sqrt{4^2-4\left(m-4\right)}+1=0\)
\(\Leftrightarrow\sqrt{32-4m}=3-m\) \(\Leftrightarrow\left\{{}\begin{matrix}32-4m=9-6m+m^2\\m\le3\end{matrix}\right.\) \(\Leftrightarrow m=1-2\sqrt{6}\)
TH2:\(x_1< x_2\)
(*)\(\Leftrightarrow\)\(x_1x_2-\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}+1=0\)
\(\Leftrightarrow m-4+1=\sqrt{32-4m}\) \(\Leftrightarrow\left\{{}\begin{matrix}m-3\ge0\\\left(m-3\right)^2=32-4m\end{matrix}\right.\)\(\Leftrightarrow m=1+2\sqrt{6}\) (tm đk m<8)
Vậy \(\left[{}\begin{matrix}m=1-2\sqrt{6}\\m=1+2\sqrt{6}\end{matrix}\right.\)
giải thích cho mình vì sao biến đổi đc từ
m−4+√42−4(m−4)+1 thành √32−4m
Lời giải:
a) Để pt có 2 nghiệm phân biệt thì:
$\Delta'=16-4m^2>0\Leftrightarrow m^2< 4\Leftrightarrow -2< m< 2$
b) Để pt có 2 nghiệm phân biệt thì:
$\Delta'=(m-1)^2>0\Leftrightarrow m\neq 1$