Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

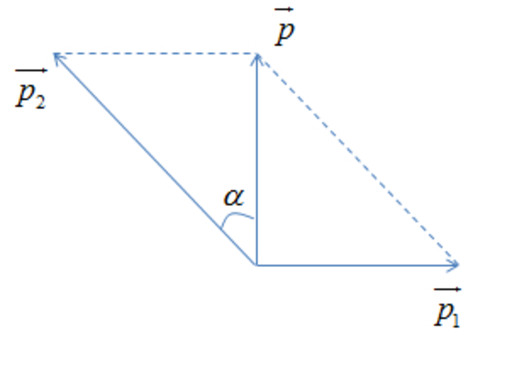
Bảo toàn động lượng ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_1^2+p_2^2+2\cdot p_1\cdot p_2\cdot cos\left(\overrightarrow{p_1;}\overrightarrow{p_2}\right)\) (1)
Có \(p=m\cdot v=2\cdot250=500\)kg.m/s
\(p_1=m_1\cdot v_1=1\cdot250=250kg.\)m/s
\(\left(1\right)\Rightarrow500^2=250^2+p_2^2+2\cdot250\cdot p_2\cdot cos60^o\)
\(\Rightarrow187500=p_2^2+250p_2\)
\(\Rightarrow\left[{}\begin{matrix}p_2\approx325,7\\p_2\approx-575,7\left(loại\right)\end{matrix}\right.\)
Theo hình ta có:
\(p_1\cdot cos\alpha=p_2\cdot sin\beta\)
\(\Rightarrow sin\beta=\dfrac{p_1\cdot cos\alpha}{p_2}=\dfrac{250\cdot cos\left(90-30\right)}{325,7}=0,38\)
\(\Rightarrow\beta\approx22,57^o\)
Mảnh thứ hai bay theo góc \(22,57^o\)

bài này đã cho bạn cái sườn hồi tối rồi :D xin phép giải vắn tắt nhất
\(p_2=\sqrt{p^2+p_1^2-2.p.p_1.\cos\left(45^0\right)}\) \(=\sqrt{\left(mv\right)^2+\left(m1v1\right)^2-2mv\left(m1v1\right)\dfrac{\sqrt{2}}{2}}\)
\(\Rightarrow p_2=m_2v_2\simeq999,14\left(kg.m/s\right)\)\(\Rightarrow v_2=\dfrac{p_2}{m_2}\simeq999,14\left(m/s\right)\) :D
\(\cos\beta=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}\) thay số nốt :D
mọi thắc mắc truy cập:
https://hoc24.vn/cau-hoi/mot-vien-dan-co-khoi-luong-3kg-bay-len-theo-phuong-thang-dung-voi-v-471ms-thino-thanh-2-manh-manh-1-co-khoi-luong-3kg-van-toc-overrightarrowv-1-chech-theo-phuong-thang-dung-1-goc-450-voi-d.334563063787

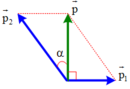
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 2.250 = 500 k g . m / s p 1 = m 1 v 1 = 1.500 = 500 k g . m / s p 2 = m 2 v 2 = v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 k g m / s
+ Mà sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 ° với vận tốc 500 2 m / s (m/s)
Chọn đáp án A

Tham khảo:
Giải thích các bước giải:
m=2kg;v=250m/s;v1=500m/s;α1=600
Bảo toàn động lượng của viên đạn trước và sau khi nổ:
P→=P1→+P2→
ta thấy:
P=m.v=2.250=500kg.m/s
P1=m1.v1=22.500=500kg.m/s
Theo quy tắc hình bình hành ta có:
(P1→;P2→)=600^;P1=P⇒P1=P2=P
Vận tốc mảnh thứ 2:
{P1=P2m1=m2
{P1=P2m1=m2
⇒v1=v2=500m/s
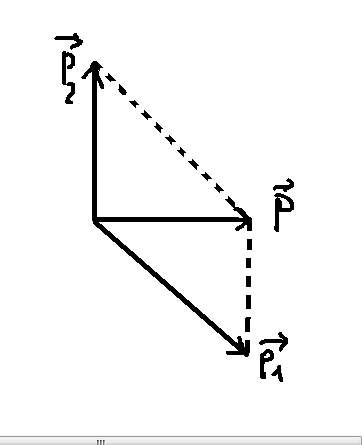
Bảo toàn động lượng: \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Quy tắc hình bình hành:
\(p_2^2=p_1^2+p^2-2p_1\cdot p\cdot cos\left(\overrightarrow{p_1};\overrightarrow{p}\right)\)
\(=\left(1\cdot500\right)^2+\left(2\cdot250\right)^2-2\cdot\left(1\cdot500\right)\cdot\left(2\cdot250\right)\cdot cos60^o\)
\(=250000\) \(\Rightarrow p_2=500kg.m\)/s
Mảnh thứ hai bay theo góc:
\(sin\alpha=\dfrac{p_1\cdot cos\left(90-30\right)}{p_2}=\dfrac{1\cdot250\cdot cos60}{500}=0,25\)
\(\Rightarrow\alpha\approx14,5^o\)

Nội lực lớn hơn ngoại lực=> động lượng được bảo toàn
Mảnh thứ nhất bay theo phương ngang với vận tốc 500m/s so với mặt đất???
Áp dụng định luật bảo toàn động lượng:
\(M.\overrightarrow{v}=m_1.\overrightarrow{v_1}+m_2.\overrightarrow{v_2}\)
\(\Leftrightarrow250.2=500.1+1.v_2\)
\(\Leftrightarrow v_2=0\left(m/s\right)\)


Refer:
\(m=2kg,v=250m/s,v_1=250m/s,α=60^o \)
Động lượng của viên đạn ban đầu:
\(p=m.v=2.250=500kg.m/s\)Động lượng của các mảnh :\(p_1=m_1.v_1=\dfrac{2}{2}.250=250(kg.m/s)\)
\(p_2=m_2.v_2=\dfrac{2}{2}.v_2=v_2(kg.m/s)\)
theo quy tắc hình bình hành ta có:
\(p_2=\sqrt{p_2+p^2_1+2.p.p_1.cosα}\)
\(=\sqrt{500^2+250^2+2.500.250.cos60}\)
\(=661,4(kg.m/s)\)
Vận tốc của mảnh 2:
\(p_2=v_2\Rightarrow v_2=661,4m/s\)Bay theo phương hợp với phương thẳng đứng:\(\dfrac{P}{sin α}=\dfrac{P_1}{sin β} \)
\(\Rightarrow sinβ=\dfrac{sin60.250}{500}=\dfrac{\sqrt{3}}{4} \)
\(\Rightarrow β=25^o39' \)
dạng này mình mới làm xong một bài nhé, bạn có thể lướt xuống tham khảo rồi áp dụng, không nên đăng cùng một loại câu hỏi nhiều lần