Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)

1:
a: 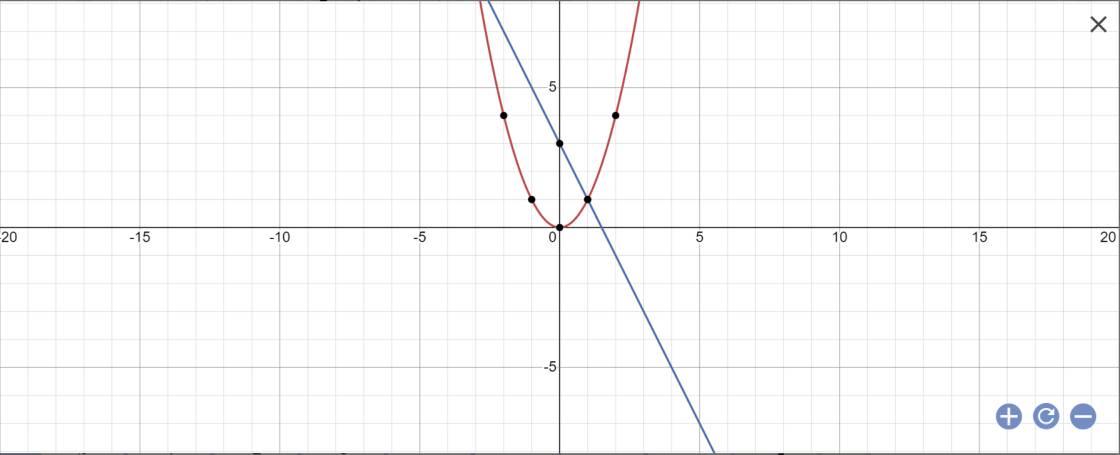
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1

a) x 2 – x – 2 = 0
Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.
Vậy tập nghiệm của phương trình là S = {-1; 2}
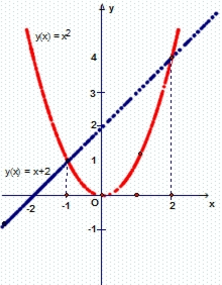
b) + Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).
+ Parabol y = x 2 đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).
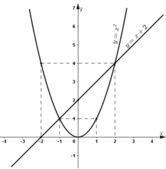
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
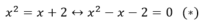
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị

a, tự tìm tự vẽ
b, Ta có : \(\hept{\begin{cases}y=x^2\\y=-x+2\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2+x-2=0\\y=-x+2\end{cases}}\)
\(\left(1\right)\Rightarrow\Delta=1+8=9>0\)
\(x_1=\frac{-1-3}{2}=-2;x_2=\frac{-1+3}{2}=1\)
Với x = -2 => \(y=2+2=4\)
Với x = 1 => \(-1+2=1\)
Vậy giao điểm của 2 đồ thị trên là A ( -2 ; 4 ) ; B ( 1 ; 1 )

a:
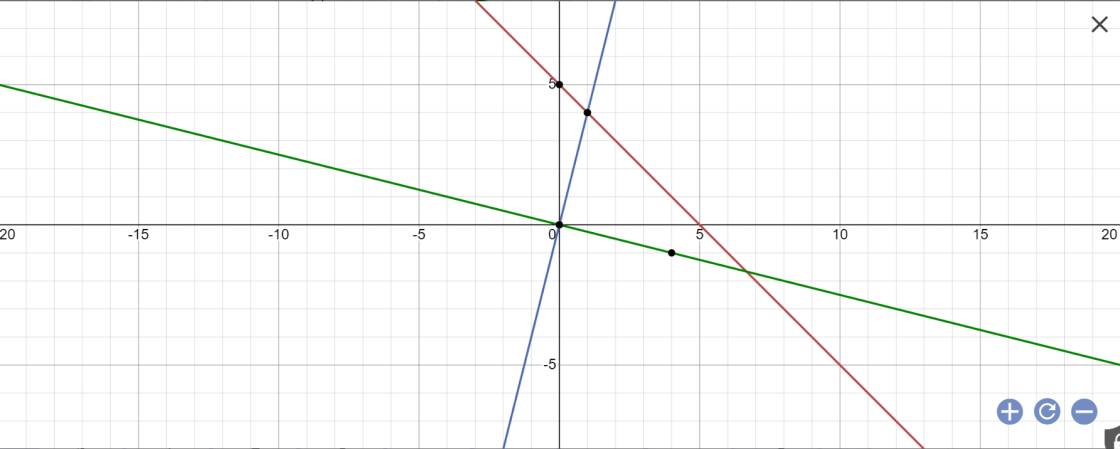
b: tọa độ A là;
-x+5=4x và y=4x
=>x=1 và y=4
Tọa độ B là;
-x+5=-1/4x và y=-1/4x
=>-3/4x=-5 và y=-1/4x
=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3
=>B(20/3;-5/3)
c: O(0;0); A(1;4); B(20/3;-5/3)
\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)
\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)
\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)
=>góc AOB tù
=>ΔOAB tù

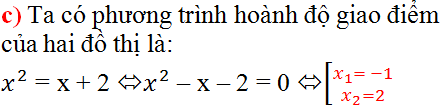

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\8y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-2y=3\\y=-1\end{matrix}\right.\)