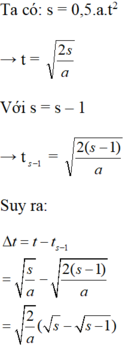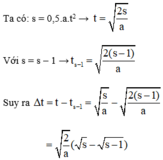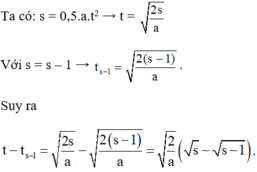Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi t là thời gian đi cả quãng đường.
\(t_1\) là thời gian đi \(\dfrac{1}{4}\) đoạn đường đầu.
Ta có: \(S=\dfrac{1}{2}at^2\)
\(\dfrac{1}{4}S=\dfrac{1}{2}at^2_1\)
\(\Rightarrow\dfrac{S}{\dfrac{1}{4}S}=\dfrac{\dfrac{1}{2}at^2}{\dfrac{1}{2}at^2_1}=\dfrac{t^2}{t^2_1}\)\(\Rightarrow t_1=\dfrac{t}{2}\)
Thời gian vật đi \(\dfrac{3}{4}\) đoạn đường cuối:
\(t'=t-t_1=t-\dfrac{t}{2}=\dfrac{t}{2}\left(h\right)\)


+ Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
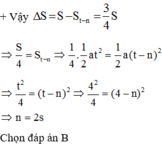

Giải: Ta có v 0 = 0 ( m / s )
Gọi t là thời gian vật đi hết quãng đường S nên t=4s, thời gian để vật đi hết 3 4 quãng đường cuối là n
Vậy Δ S = S − S t − n = 3 4 S ⇒ S 4 = S t − n ⇒ 1 4 . 1 2 a t 2 = 1 2 a ( t − n ) 2 ⇒ t 2 4 = ( t − n ) 2 ⇒ 4 2 4 = ( 4 − n ) 2 ⇒ n = 2 s

Chọn gốc tọa độ tại nơi vật bắt đầu xuất phát, mốc thời gian từ lúc vật bắt đầu chuyển động, chiều dương là chiều chuyển động.
(Thời gian đi 3/4 quãng đường cuối = thời gian đi cả quãng đường - thời gian đi 1/4 quãng đường đầu)
Ta có:
- Cả quãng đường đi với thời gian là t (giây):
\(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}at^2\) (*)
\(\frac{1}{4}s=v_0t'+\frac{1}{2}a\left(t'\right)^2=\frac{1}{2}a\left(t'\right)^2\) (**)
(Vì v(0) = 0)
Lấy (*) chia (**) \(\frac{t^2}{\left(t'\right)^2}=4\Rightarrow t'=\frac{1}{2}t\)
Thời gian đi 3/4 quãng đường cuối là:
\(t''=t-t'=t-\frac{1}{2}t=\frac{1}{2}t\)
+ Thời gian đi đoạn đường S là 6s.
+ Tìm thời gian đi 1/4 đoạn đường S ban đầu là t1
+ Từ đó suy ra thời gian đi 3/4 đoạn đường sau là: t2 = 6 - t1