Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách tử ảnh đến thấu kính:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow d'=\dfrac{d.f}{d-f}=\dfrac{3.2}{3-2}=6\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{6.2}{3}=4\left(cm\right)\)

a,vì d>f(3cm>2cm) nên vật cho ảnh thật ngược chiều và lớn hơn vật
b,ta có 1/f=1/d+1/d'<=>1/2=1/3+1/d'<=>d'=6cm(f là tiêu cự,d và d' lần lượt là khoảng cách từ vật và ảnh tới thấu kính)=> khoảng cách từ ảnh tới thấu kính tới thấu kính là 6cm
đổi 1m=100cm ta có h/h'=d/d'<=>100/h'=3/6<=>h'=200cm(h và h' lần lượt là chiều cao của vật AB và chiều cao của ảnh A'B')
Vậy độ lớn của ảnh là 200cm

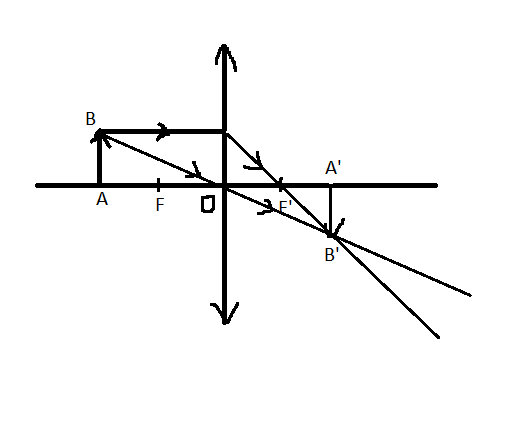
Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{15}{30}\Rightarrow h'=4cm\)


Đặc điểm:
- Ảnh thật
- Ảnh lớn hơn vật và ngược chiều với vật
Tóm tắt:
AB = h = 2cm
OF = OF' = f = 8cm
AO = d = 12cm
A'B' = h = ?
A'O = d' = ?
Giải:
\(\Delta ABF\sim\Delta OIF\)\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{AO-OF}{OF}\Leftrightarrow\dfrac{2}{A'B'}=\dfrac{12-8}{8}\)
\(A'B'=\dfrac{2.8}{12-8}=4cm\)
\(\Delta ABO\sim\Delta A'B'O\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\Leftrightarrow\dfrac{2}{4}=\dfrac{12}{A'O}\Rightarrow A'O=\dfrac{12.4}{2}=24cm\)

Đặc điểm:
- Ảnh ảo
- Ảnh lớn hơn vật và cùng chiều với vật
Tóm tắt:
AB = h = 2cm
OF = OF' = f = 8cm
AO = d = 6cm
A'B' = ?
A'O = ?
Giải:
\(\Delta OFI\sim\Delta AFB\)
\(\Rightarrow\dfrac{OF}{AF}=\dfrac{OI}{AB}\Leftrightarrow\dfrac{OF}{OF-OA}=\dfrac{A'B'}{AB}\Leftrightarrow\dfrac{8}{8-6}=\dfrac{A'B'}{2}\)
\(\Rightarrow A'B'=\dfrac{8.2}{8-6}=8cm\)
\(\Delta A'B'O\sim\Delta ABO\)
\(\Rightarrow\dfrac{A'B'}{AB}=\dfrac{A'O}{AO}\Leftrightarrow\dfrac{8}{2}=\dfrac{A'O}{6}\Rightarrow A'O=\dfrac{8.6}{2}=24cm\)
