Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Câu này đề bài là: \(\lim\limits_{x\rightarrow1}\dfrac{x-\sqrt[]{x+2}}{x-\sqrt[3]{3x+2}}\) đúng ko nhỉ?
Vậy thay số là được: \(=\dfrac{1-\sqrt[]{1+2}}{1-\sqrt[3]{3+2}}=\dfrac{1-\sqrt[]{3}}{1-\sqrt[3]{5}}\)
2.
a. \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
b.
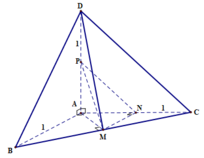
Trong mp (ABCD), từ D kẻ \(DE\perp AC\) (1)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp DE\) (2)
(1);(2) \(\Rightarrow DE\perp\left(SAC\right)\Rightarrow SE\) là hình chiếu vuông góc của SD lên (SAC)
\(\Rightarrow\widehat{DSE}\) là góc giữa SD và (SAC) hay \(\widehat{DSE}=\alpha\)
\(AC=\sqrt{AB^2+AD^2}=a\sqrt{5}\)
Áp dụng hệ thức lượng trong tam giác vuông ADC:
\(AE.AC=AD^2\Rightarrow AE=\dfrac{AD^2}{AC}=\dfrac{4a\sqrt{5}}{5}\)
\(SE=\sqrt{SA^2+AE^2}=\dfrac{a\sqrt{105}}{5}\) ; \(SD=\sqrt{SA^2+AD^2}=a\sqrt{5}\)
\(\Rightarrow cos\alpha=\dfrac{SE}{SD}=\dfrac{\sqrt{21}}{5}\)

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-\left(x+1\right)}{2x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{x^2+1}-\left(x+1\right)\right)\left(\sqrt{x^2+1}+x+1\right)}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2x}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2}{\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\dfrac{-2}{\left(0-1\right)\left(\sqrt{1}+1\right)}=1\)
a. \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{x+2}=\dfrac{1}{4}\)
b. \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}=\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}\)
Do \(\lim\limits_{x\rightarrow3^-}\left(-x-3\right)=-6< 0\)
\(\lim\limits_{x\rightarrow3^-}\left(3-x\right)=0\) và \(3-x>0;\forall x< 3\)
\(\Rightarrow\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}=-\infty\)
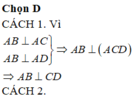

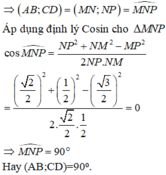



1:
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{2-5x}+2}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{10-5x}{\left(x-2\right)\left(\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4\right)}=\lim\limits_{x\rightarrow2}\dfrac{-5}{\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4}=-\dfrac{5}{4}\)
Làm bài 2 chưa bạn gửi mình với