Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 15p = \(\frac{1}{4}\)h
Gọi vận tốc ca nô khi dòng nước yên lặng là x (km/h) ĐK: x > 0
Vận tốc của ca nô khi xuôi dòng: x + 4 (km/h)
Vận tốc của ca nô khi ngược dòng: x - 4 (km/h)
Thời gian ca nô xuôi dòng : \(\frac{80}{x+4}\)(h)
Thời gian ca nô ngược dòng : \(\frac{72}{x-4}\)(h)
Ta có PT: \(\frac{72}{x-4}-\frac{80}{x+4}=\frac{1}{4}\)
\(\Leftrightarrow\frac{288\left(x+4\right)-320\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\frac{x^2-16}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2+32x-2448=0\)
Giai PT ta được x1 = 36 (Nhận)
x2 = -68 (Loại)
Vậy vận tốc thực của ca nô là 36km/h

Gọi vận tốc thực của ca nô là x (x > 0, km/h)
Đổi 15 phút = 15 60 = 1 4 h
*) Xuôi dòng:
Vận tốc của ca nô là x + 4 (km/h) → Thời gian xuôi dòng của ca nô là 80/(x+4) (h)
*) Ngược dòng
Vận tốc ngược dòng của ca nô là x – 4 (km/h) → Thời gian ngược dòng của ca nô là 72/(x-4) (h)
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
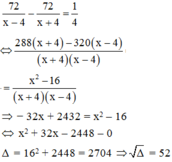
Phương trình có hai nghiệm
x = −16 + 52 = 36 (tmdk)
x = −16 – 52 = −68 (loại)
Vậy vận tốc thực của ca nô là 36 km/h
Đáp án: A

Gọi vận tốc riêng của cano là \(x\left(km/h\right),x>4\).
Vận tốc khi cano đi xuôi dòng là: \(x+4\left(km/h\right)\).
Thời gian cano đi xuôi dòng là: \(\frac{120}{x+4}\left(h\right)\).
Vận tốc khi cano đi ngược dòng là: \(x-4\left(km/h\right)\).
Thời gian cano đi ngược dòng là: \(\frac{96}{x-4}\left(h\right)\).
Ta có phương trình:
\(\frac{96}{x-4}-\frac{120}{x+4}=1\)
\(\Rightarrow96\left(x+4\right)-120\left(x-4\right)=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2+24x-880=0\)
\(\Leftrightarrow x=20\)(vì \(x>4\))
.

Gọi vận tốc riêng của canoo là x ( x>0
vận tốc cano đi xuôi là x + 4 (km/h)
thời gian cano đi xuôi là : \(\frac{80}{x+4}\)km/ h
vận tốc cano đi ngc là ; x - 4 (km/h)
thời gian cano đi ngc hết là \(\frac{72}{x-4}\)
ta lại có thời gian khi đi xuôi ít hơn thời gian đi ngc là 15 ph= \(\frac{1}{4}\)h
\(\Rightarrow\)pt \(\frac{80}{x+4}\)+\(\frac{1}{4}\)=\(\frac{72}{x-4}\)
giải ra ta đc x = 36

Gọi vận tốc canoo là x ( x > 0 )
Theo bài ra ta có pt \(4\left(x+4\right)=5\left(x-4\right)\Leftrightarrow4x+16=5x-20\Leftrightarrow x=36\left(tm\right)\)
Quãng đường AB là 4 . 40 = 160 km

Gọi vận tốc riêng của cano là x (x>3)
Vận tốc khi chạy xuôi dòng: x+3 (km/h)
Vận tốc khi chạy ngược dòng: x-3 (km/h)
Thời gian khi chạy xuôi dòng: \(\dfrac{72}{x+3}\) (h)
Thời gian khi chạy ngược dòng: \(\dfrac{54}{x-3}\) (h)
Vì thời gian chạy hết tất cả 6h nên ta có phương trình:
\(\dfrac{72}{x+3}\) + \(\dfrac{54}{x-3}\) =6
⇔72.(x-3) + 54.(x+3)=6.(x2-9)
⇔72x-216+54x+162=6x2-54
⇔6x2-126x=0
⇔x.(6x-126)=0
⇔x=0 (loại) hoặc x=21 (thỏa mãn)
Vậy vận tốc riêng của tàu thủy là 21 km/h

Gọi vận tốc riêng của tàu thủy là v (v > 3; km/h).
Theo bài ra ta có: \(\dfrac{72}{v+3}+\dfrac{54}{v-3}=6\)
\(\Leftrightarrow\dfrac{12}{v+3}+\dfrac{9}{v-3}=1\Leftrightarrow\dfrac{21v-9}{v^2-9}=1\Leftrightarrow v^2=21v\Leftrightarrow v=21\). (TM)
Vậy ..
Lời giải:
Gọi vận tốc tàu là $a$ và vận tốc dòng là $b$ (km/h)
Vận tốc xuôi dòng: $a+b$ (km/h)
Vận tốc ngược dòng: $a-b$ (km/h)
Thời gian xuôi dòng: $\frac{160}{a+b}$ (giờ)
Thời gian ngược dòng: $\frac{144}{a-b}$ (giờ)
Theo bài ra ta có: $\frac{160}{a+b}+0,5=\frac{144}{a-b}$
Đến đây có thể tìm mối quan hệ của $a,b$ chứ không tính được $a,b$ cụ thể. Bạn xem lại đề xem có sót dữ kiện nào không nhé.