Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian đi từ A đến B với vận tốc 40km/h nhiều hơn thời gian đi với vận tốc 50 km/h là:
10 + 5 = 15 phút
Trên cùng một quãng đường, thời gian tỉ lệ nghịch với vận tốc nên tỉ số thời gian đi với vận tốc 40 km/h và đi với vận tốc 50km/h là: 50/40 = 5/4
Bài toán Hiệu - tỉ:
Thời gian đi với vận tốc 40 km/h là 5 phần, đi với vận tốc 50 km/h là 4 phần
Hiệu số phần bằng nhau là:
5 - 4 = 1 phần
Thời gian người đo đi từ A đến B với vận tốc 40 km/h là:
15 : 1 x 5 = 75 (phút) = 1,25 giờ
Quãng đường AB dài là:
1,25 x 40 = 50 (km)
Đáp số: 50 km
Tỉ số vận tốc khi đi chậm và khi đi nhanh:
40/50=4/5
Cùng một quãng đường thì tỉ số vận tốc tỉ lệ nghịch với tỉ số thời gian, do đó tỉ số thời gian khi đi chậm và đi nhanh: 5/4
Hiệu thời gian giữa hai lần đi chậm và nhanh là:
10 +5=15 phút =1/4 giờ
ta có sơ đồ thời gian đi chậm và nhanh:
I---I---I---I---I---I
I---I---I---I---I
Giá trị một phần dễ thấy là 15 phút hay 1/4 giờ
Theo sơ đồ ta dễ thấy giá trị một phần là 15 phút hay 1/4 giờ
Vậy thời gian mất khi đi nhanh:
1/4 x 4 = 1 giờ
Vậy quãng đường AB:
1 x 50 =50 km
Đáp số:50 km
Vào lúc: 2016-03-11 20:42:58 Xem câ

Tỉ số vận tốc khi đi chậm và khi đi nhanh:
\(\frac{40}{50}=\frac{4}{5}\)
Vì cùng một quãng đường thì tỉ số vận tốc tỉ lệ nghịch với tỉ số thời gian
Do đó tỉ số thời gian khi đi chậm và đi nhanh là: \(\frac{5}{4}\)
Hiệu thời gian giữa hai lần đi chậm và nhanh là:
10+5=15phút
Đổi 15 phút=\(\frac{1}{4}\) giờ
Ta có sơ đồ thời gian đi chậm và nhanh:
I---I---I---I---I---I
I---I---I---I---I
Giá trị một phần dễ thấy là 15phút hay \(\frac{1}{4}\) giờ
Vậy thời gian mất khi đi nhanh:
\(\frac{1}{4}\)x4=1(giờ)
Vậy quãng đường AB:
1x50=50(km)
Đáp số:50 km

Gọi vận tốc ban đầu của người đó là x>0 (km/h)
Thời gian dự định đi hết quãng đường: \(\frac{120}{x}\) giờ
Quãng đường còn lại sau khi đi 1h: \(120-x\) (km)
Thời gian đi hết quãng còn lại: \(\frac{120-x}{x+6}\)
Ta có pt:
\(\frac{120}{x}-\left(1+\frac{1}{6}+\frac{120-x}{x+6}\right)=0\)
\(\Leftrightarrow720\left(x+6\right)-7x\left(x+6\right)-6x\left(120-x\right)=0\)
\(\Leftrightarrow-x^2-42x+4320=0\Rightarrow\left[{}\begin{matrix}x=48\\x=-90\left(l\right)\end{matrix}\right.\)

Thời gian để ô tô gặp xe máy là:
132.8:(48+35)=8/5 (giờ)=96 (phút)=1 giờ 36 phút
ĐS:1 giờ 36 phút

Thời gian hai xe gặp nhau là:
24:(48-32)=3/2 giờ=1 giờ 30 phút
Lúc đó là:
6h45'+1h30'=8h15'

Tham khảo:
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ
Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)
Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)
Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)
Như vậy hàm số tính quãng đường s (km) sau t phút là:
\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)
b)
Với \(0 \le t \le 90\) thì \(s = 0,7t\)
Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)
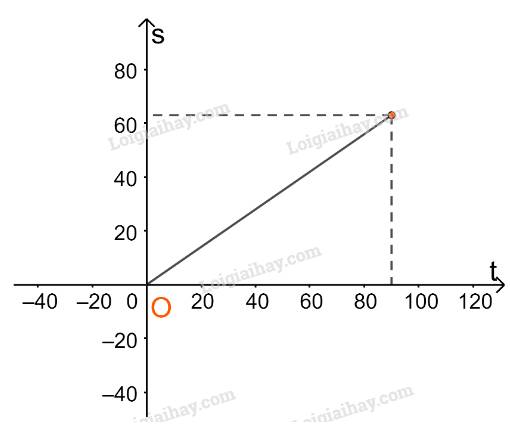
Với \(90 < t \le 105\) thì \(s = 63(km)\)
Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)
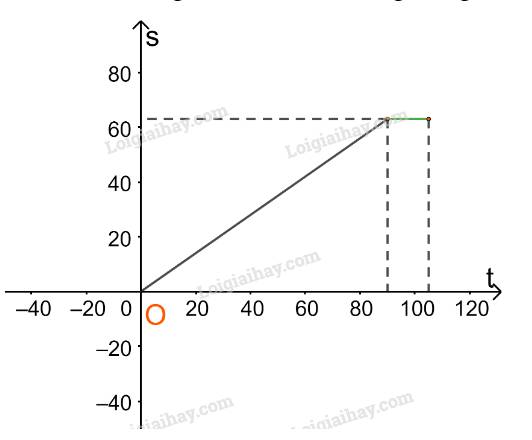
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)
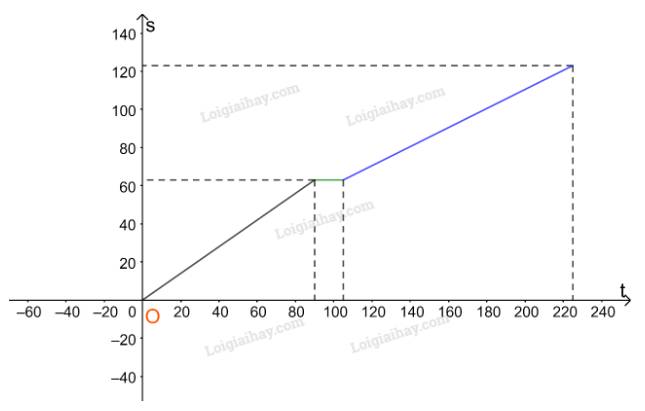
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.
Gọi vận tốc ban đầu là x ( km/h ) ( x > 0 )
Khi đó :
Vận tốc khi tăng tốc là: x + 4 ( km/h )
Thời gian người đó đi dự tính là: \(\dfrac{90}{x}\)
Thời gian đi thực tế là : \(\dfrac{90-x}{x+4}\)
Theo đề bài ta có: \(\dfrac{90}{x}-\dfrac{9}{60}=1+\dfrac{90-x}{x+4}\)
⇒ 90.60( x + 4 ) - 9x ( x + 4 ) = 60x ( x + 4 ) + 60x( 90 - x )
Xong giải ra là ra.