Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc trung bình của ô tô trên cả đoạn đường là
\(v_{tb}=\dfrac{\left(v_1+v_2+v_3\right)}{3}=\dfrac{12+8+16}{3}=12\left(ms\right)\)
Đổi 12m/s = 43,2 kmh
Vận tốc trung bình của ô tô trên cả chặng đường là:
\(V_{tb}=\dfrac{2v_1.\left(v_2+v_3\right)}{2v_1+v_2+v_3}=\dfrac{2.12\left(8+16\right)}{2.12+8+16}=12\dfrac{m}{s}\)

Vận tốc trung bình của ô tô trên cả chặng đường là
\(v_{tb}=\dfrac{v_1+v_2+v_3}{3}=\dfrac{12+8+16}{3}=12\left(ms\right)\)

Chặng đường gồm ba giai đoạn liên tiếp cùng chiều dài nên s1 = s2 = s3 = s.
Thời gian ô tô chuyển động trên mỗi chặng lần lượt là:
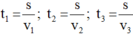
Vận tốc trung bình của ô tô trên cả chặng đường là:
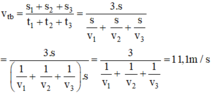

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
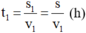
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
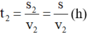
Vậy tổng thời gian đi hết cả quãng đường là: 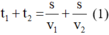
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
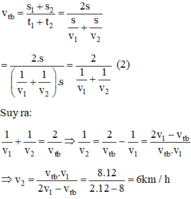

Vận tốc người đi xe đạp đi nửa quãng đường còn lại là:
\(v_{tb}=\dfrac{2}{\dfrac{1}{12}+\dfrac{1}{v_2}}=\dfrac{2}{\dfrac{1}{4}}=8\left(\dfrac{km}{h}\right)\)
=> \(\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\) => \(v_2=6\left(\dfrac{km}{h}\right)\)
Đáp số: 6 km/h.
Vtb = (S1 + S2)/(t1 + t2)=2S1/(S1/V1 + S2/V2) = 2/(1/V1 + 1/V2) ( cùng rút gọn cho S1)
<=> 8 = 2/(1/12 + 1/V2) => V2 = 6 (km/h)
Vậy vận tốc trên quãng đường còn lại là 6km/h.

\(=>vtb=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{v2}}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{2v2}}=\dfrac{S}{\dfrac{S\left(2v2+40\right)}{80v2}}=\dfrac{80v2}{2v2+40}=15\)
\(=>v2=12km/h\)

mÌNH MỎI TAY QUÁ
Lấy gốc tọa độ tại AA chiều dương là chiều từ AA đến BB. Gốc thời gian là lúc 7h7h
Phương trình chuyển động của :
Xe đi từ A:A: xA=36t(km−h)xA=36t(km−h)
Xe đi từ B:xB=96−28t(km−h)B:xB=96−28t(km−h)
Hai xe gặp nhau khi :xA=xB:xA=xB
→36t=96−28t→36t=96−28t
⇒t=1,5(h)⇒t=1,5(h)
xA=36t=36.1,5=54(km)xA=36t=36.1,5=54(km)
Hai xe gặp nhau lúc 8h30′8h30′. Nơi gặp nhau cách AA 54km54km
TH1:TH1: Hai xe cách nhau 24km24km trước khi hai xe gặp nhau
Hai xe cách nhau 24km
⇔⇔ xB−xA=24xB−xA=24
⇔⇔ 96−28t′−36t′=2496−28t′−36t′=24
⇔t′=1,125h⇔t′=1,125h
Vậy lúc 8h7phút30giây hai xe cách nhau 24km
TH2:TH2: Hai xe cách nhau 24k sau khi gặp nhau
Hai xe cách nhau 24km
⇔xA−xB=24⇔xA−xB=24
⇔36t′′−96+28t′′=24⇔36t″−96+28t″=24
⇔t′′=1,875(h)⇔t″=1,875(h)
Vậy lúc 8h52phút30giây hai xe cách nhau 24km
bài 2:
ta có:
thời gian người đó đi trên nửa quãng đường đầu là:
t1=S1/v1=S/2v1=S/24
thời gian người đó đi hết nửa đoạn quãng đường cuối là:
t2=S2/v2=S2/v2=S/40
vận tốc trung bình của người đó là:
vtb=S/t1+t2=S/(S/40+S/24)=S/S(140+124)=1/(1/24+1/40)
⇒vtb=15⇒vtb=15 km/h
bài 3:
thời gian đi nửa quãng đầu t1=(1/2) S.1/25=S/50
nửa quãng sau (1/2) t2.18+(1/2) t2.12=(1/2) S⇔t2=S/30
vận tốc trung bình vtb=S/(t1+t2)=S/S.(1/50+1/30)=1/(1/50+1/30)=18,75(km/h)
HT
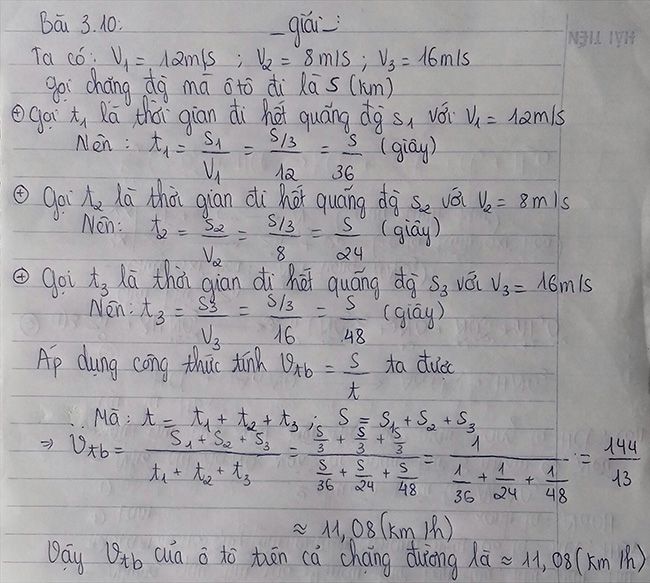
2) Gọi S là chiều dài của 1 đoạn đường.
Thời gian ô tô đi hết đoạn 1 là : \(t_1=\frac{S}{v_1}=\frac{S}{12}\left(s\right)\)
Thời gian ô tô đi hết đoạn 2 là: \(t_2=\frac{S}{v_2}=\frac{S}{8}\left(s\right)\)
Thời gian ô tô đi hết đoạn 3 là : \(t_3=\frac{S}{v_3}=\frac{S}{16}\left(s\right)\)
Vận tốc trung bình của ô tô trên cả chặng đường :
\(v_{tb}=\frac{S+S+S}{t_1+t_2+t_3}=\frac{3S}{\frac{S}{12}+\frac{S}{8}+\frac{S}{16}}\)
\(\Leftrightarrow v_{tb}=\frac{3}{\frac{1}{12}+\frac{1}{8}+\frac{1}{16}}=\frac{3}{\frac{13}{48}}\)
\(\Rightarrow v_{tb}=\frac{144}{13}\left(\frac{m}{s}\right)\)
1) Gọi S là chiều dài quãng đường người đó phải đi
Thời gian người đó đi hết nửa quãng đường đầu: \(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{2.12}=\frac{S}{24}\left(h\right)\)
Thời gian người đó đi hết quãng đường còn lại: \(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\left(h\right)\)
Theo bài ra ta có:
\(v_{tb}=\frac{S_1+S_2}{t_1+t_2}=\frac{S}{\frac{S}{24}+\frac{S}{2v_2}}=\frac{2.24.v_2}{24+v_2}=\frac{48.v_2}{24+v_2}\)
\(\Leftrightarrow8=\frac{48v_2}{24+v_2}\Leftrightarrow8\left(24+v_2\right)=48v_2\)
\(\Leftrightarrow192+8v_2=48v_2\Leftrightarrow40v_2=192\)
\(\Rightarrow v_2=\frac{192}{40}=4,8\left(\frac{km}{h}\right)\)