Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Diện tích mặt đáy:
\(S=\dfrac{V}{h}=\dfrac{2x^3+6x^2-8x}{2x}=\left(2x^3:2x\right)+\left(6x^2:2x\right)-\left(8x:2x\right)=x^2+3x-4\)
b, \(h=10\left(dm\right)\\ \Leftrightarrow 2x=10\left(dm\right)\\ \Leftrightarrow x=5\left(dm\right)\\ \Rightarrow S=x^2+3x-4\left(dm^2\right)=5^2+3.5-4=36\left(dm^2\right)\\ V=2x^3+6x^2-8x\left(dm^3\right)=2.5^3+6.5^2-8.5=360\left(dm^3\right)\)

`a)`
Biểu thức biểu thị V của hình HCN là:
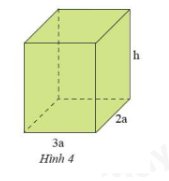
`3a*2a*h = 6a^2 * h` `(cm^3)`
Biểu thức biểu thị S xung quanh của HCN là:
`(3a+2a)*2*h = 5a*2*h = 10a*h` `(cm^2)`
`b)`
Thay `a = 2` cm; `h = 5` cm
V của hình HCN đó là:
`6*2^2 * 5 = 24 * 5 =120 (cm^3)`
S xung quanh của hình HCN đó là:
`10*2*5 = 10*10 = 100 (cm^2)`
Vậy: `a) 6a^2 * h`; `10a*h`
`b) 120` `cm^3;` `100` `cm^2.`
`a,` Thể tích: `V = h . 2a . 3a = 6a^2h`.
Diện tích xung quanh: `S_(xq) = (3ah+2ah) xx 2 = 10ah`.
`b, V = 6 . 2^2 . 5 = 120 cm^2`
`S = 10 . 2 . 5 = 100 cm^2`

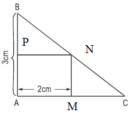
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
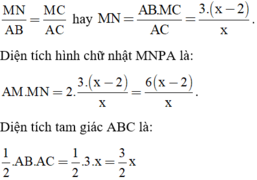
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
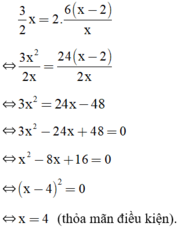
Vậy độ dài đoạn thẳng AC là 4cm.

s xung quanh là :
[40 + 30] * 2 * 45 = 6300 [ cm2 ]
Thể tích là :
40 * 30 * 45 = 54000 [ cm3]
Vẽ hình thì bn tự vẽ nha , nhớ k mk đó thanks

Đáp án B
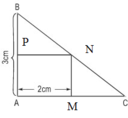
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
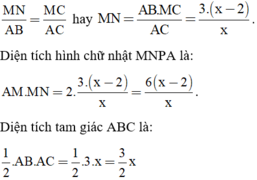
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
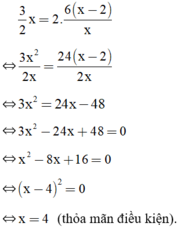
Vậy độ dài đoạn thẳng AC là 4cm.
Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2