Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. a) Tập xác định: D = R;
y' = 3 – 2x => y' = 0 ⇔ x = 3/2
Ta có Bảng biến thiên:

Hàm số đồng biến trên khoảng (-∞; 3/2); nghịch biến trên khoảng (3/2; +∞).
b) Tập xác định: D = R;
y' = x2 + 6x – 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên:

Hàm số đồng biến trên các khoảng (-∞; -7), (1; +∞); nghịch biến trên các khoảng (-7; 1).
c) Tập xác định: D = R.
y' = 4x3 – 4x = 4x(x2 – 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: (Học sinh tự vẽ)
Hàm số đồng biến trên các khoảng (-1; 0), (; +∞); nghịch biến trên các khoảng (-∞; -1), (0; 1).
d) Tập xác định: D = R.
y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2/3.
Bảng biến thiên:

Hàm số đồng biến trên khoảng (0; 2/3); nghịch biến trên các khoảng (-∞; 0), (2/3; +∞).

Đặt 2x=A suy ra 4x=A2.
Do đó 4x+4-x=23 \(\Leftrightarrow\)A2+\(\frac{1}{A^2}\)=(A+\(\frac{1}{A}\))2-2=23
Do đó 2X+2-X=A+1/A=\(\sqrt{23+2}\)=5(Do A dương)
đặt \(t=4^x\)
\(\Rightarrow t+\frac{1}{t}=23\)
\(\Leftrightarrow t^2-23t+1=0\)
\(\orbr{\begin{cases}t=\frac{23+5\sqrt{21}}{2}\\t=\frac{23-5\sqrt{21}}{2}\end{cases}}\)
Vậy \(4^x=\frac{23+5\sqrt{21}}{2}\)hoặc \(4^x=\frac{23-5\sqrt{21}}{2}\)
\(\Rightarrow log_4\left(4^x\right)=log_4\left(\frac{23+5\sqrt{21}}{2}\right)\)
\(x=log_4\left(23+5\sqrt{21}\right)-log_4\left(2\right)\)
\(\Rightarrow2^{log_4\left(\frac{23+5\sqrt{21}}{2}\right)}+2^{-log_4\left(\frac{23+5\sqrt{21}}{2}\right)}\)
=5 :)) tự bấm máy tính nếu cần giải tay thì alo mình

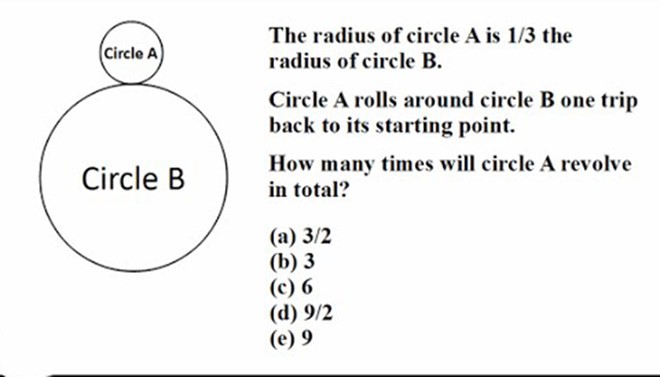
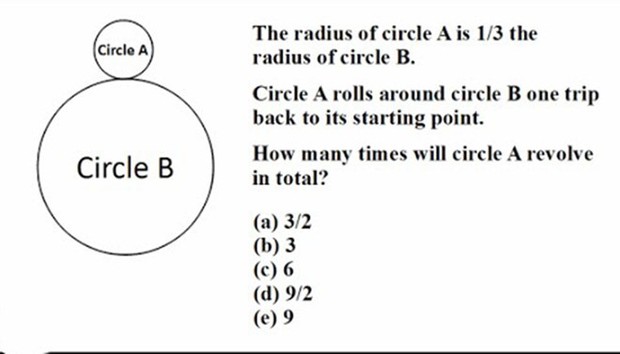
Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A.
Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A).
Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Thế nên chả có đáp án nào đúng cả

Vì tờ số 3 là số la mã còn số còn lại là stn đúng ko
Ha Hok tra Loi Nua Dau De coi Cac Ban Dung Hok
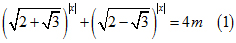 với m là tham số.
với m là tham số.
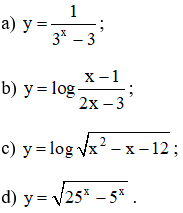

1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)