Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Độ dài cạnh là:
\(\sqrt{\dfrac{324}{4}}=9\left(cm\right)\)
Diện tích toàn phần hình lập phương:
S T P =6.(2.2) = 24 (đơn vị diện tích)
Thể tích hình lập phương:
V = 2.2.2 = 8 (đơn vị thể tích)
a. S toàn phần là 6a^2 nên cạnh hình lập phương là 6a^2=54 nên a^2 =9 nên a=3 cm
Vậy cạnh lập phương là 3 cm
b. V=a^3=6^3=216cm^3
Gọi hình thoi đó là ABCD
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH (H\(\in DC\))
a. SABCD=\(\dfrac{1}{2}.AC.BD=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là 96 cm2
b. Ta có: AO=OC=\(\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
OD=OB=\(\dfrac{BD}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\) có \(\widehat{DOA}=90^o\)
=> OD2+AO2=AD2 (định lý Py-ta-go)
hay: 82+62=AD2
=> AD2=100
=> AD=10 (cm)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c. Ta có: SABCD=AH.DC
=> AH=\(\dfrac{S_{ABCD}}{DC}=\dfrac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài đường cao của hình thoi đó là 9,6 cm
Gọi hình thoi đó là \(ABCD\)
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH \(\left(H\in DC\right)\)
a ) \(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là \(96cm^2\)
b ) Ta có : \(AO=OC=\frac{AC}{2}=\frac{12}{2}=6\left(cm\right)\)
\(OD=OB=\frac{BD}{2}=\frac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\)có \(\widehat{DOA}=90^0\)
\(\Rightarrow OD^2+AO^2=AD^2\)( định lí Py - ta - go )
Hay \(8^2+6^2=AD^2\)
\(\Rightarrow AD^2=100\)
\(\Rightarrow AD=10\left(cm\right)\)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c ) Ta có : \(S_{ABCD}=AH.DC\)
\(\Rightarrow AH=\frac{S_{ABCD}}{DC}=\frac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài dduwowgf cao của hình thoi là 9,6 cm
Chúc bạn học tốt !!!
DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. 
có AB = 3cm, AC = 4,5cm, BC = 6cm. 
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh 
. 
AC). Tính AN? 
nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng. 
có 
và 
có MN = 6cm; MP = 8cm; 
đồng dạng với 
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
gọi tên hình thoi là ABCD
áp dụng định lý Pitago trong tam giác vuông ta có
AB^2=AO^2+BO^2
=> 10^2=(16:2)^2+BO^2
=> 10^2=8^2+BO^2
=> BO^2=10^2-8^2
=> BO=6 cm
Sabcd=1/2.AC.BD=1/2.16.(2.6)=96 cm vuông
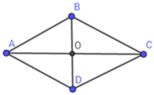
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, AB = 5 cm; BD = 6 cm.
Suy ra BO = 1 2 BD = 1 2 .6 = 3 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AO = A B 2 − O B 2 = 5 2 − 3 2 = 4
SABCD = 1 2 BD. AC = 1 2 BD. 2AO = BD.AO = 6.4 = 24 (cm2)
Đáp án cần chọn là: C
1) Một nữa độ dài đường chéo của hình thôi đã biết: \(\dfrac{24}{2}=12cm\)
Cạnh của hình thôi và một nữa độ dài đường chéo sẽ tạo nên một tam giác vuông tại giao điểm của 2 đường chéo:
Đặt A là một nữa độ dài đường chéo chưa biết.
Áp dụng định lý Pytago ta có:
\(20^2=A^2+12^2\)
\(\Rightarrow A^2=20^2-12^2=256\)
\(\Rightarrow A=\sqrt{256}=16\left(cm\right)\)
Vậy độ dài đường chéo chưa biết là: \(16.2=32\left(cm\right)\)
Diện tích hình thôi là:
\(\dfrac{1}{2}\left(32.24\right)=384\left(cm^2\right)\)
2) Độ dài cạnh của hình lập phương là:
\(\sqrt[3]{125}=5cm\)
Diện tích xung quanh của hình lập phương là:
\(5^2.4=100\left(cm^2\right)\)