Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

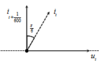
Tại thời điểm t, ta có u = U 0 = 200 2 V; thời điểm t+1/600s, ta có i=0 và đang giảm.
→ Biểu diễn vecto quay cho điện áp u tại thời điểm t và dòng điện i tại thời điểm t+1/600s.
Veto cường độ dòng điện i tại thời điểm t tương ứng với góc lùi Δ φ = 2 π f Δ t = 2 π .50. 1 600 = π 6 .
→ Dòng điện sớm pha hơn điện áp một góc π/3.
Công suất tỏa nhiệt của cuộn dây P d = P m − P R = U I cos φ − I 2 R = 200.2. cos 60 0 − 2 2 .30 = 80 W
Đáp án C

Chọn B
U RL = | · Z RL = U R 2 + Z L 2 R 2 + Z L - Z C 2 ∉ R ⇔ Z L 2 = Z L - Z C 2 ⇒ Z C = 2 Z L Z = R 2 + Z L 2 = U I = 100 Ω ⇒ Z L ≤ 100 Ω ⇒ Z C = 2 Z L ≤ 200 Ω ⇒ C ≥ 1 100 π 200 = 50 π 10 - 6 F

Chuẩn hóa R = 1.
Dòng điện trong hai trường hợp vuông pha với nhau
Z L − Z C Z L = − 1 ⇒ Z L − Z C 2 = 1 Z L 2
I 2 = 2 I 1 ⇔ Z 1 2 = 4 Z 2 2 ⇔ 1 + 1 Z L 2 = 4 + 4 Z L 2 ⇒ Z L =
→ Hệ số công suất của đoạn mạch khi không nối tắt
cos φ = R R 2 + Z L − Z C 2 = 1 5
Đáp án B

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Đáp án C
+ Ở thời điểm t: ![]()
+ Ở thời điểm ![]()
Lại có i = 0 và đang giảm
![]()
Có ![]()
![]()

Chọn A.
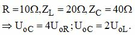
u L và u C ngược pha, có:
u L U o L = − u C U o C ⇔ 20 U o L = − u C U o C ⇒ u C = − 40 V
mạch R, L, C mắc nối tiếp nên
u = u R + u L + u C ⇔ 40 = u + R 20 − 40 ⇒ u R = 60 V
Do u R và u C vuông pha, có:
60 U o R 2 + − 40 4 U o R 2 = 1 ⇒ U o R = 10 37 V ⇒ I o = U o R R = 10 37 10 = 37 A ⇒ I = 37 2 ≈ 4 , 3 A .

Chọn B
f = f1. → Zd = R 2 + Z L 1 2 =100Ω => R 2 + Z L 1 2 = 10 4
Khi UC = UCmax thì ZC1 = R 2 + Z L 1 2 Z L 1 => L C = R 2 + Z L 1 2 = 10 4 (*)
Khi f = f2; I = Imax trong mạch có cộng hưởng điện => ZC2 = ZL2
LC = 1 ω 2 2 = 1 4 π 2 f 2 2 (**)
Từ (*) và (**) => L2 = 10 4 4 π 2 f 2 2 => L = 10 2 2 πf 2 = 1 2 π = 0 , 5 π H

Đáp án B
+ Ở thời điểm t: u A B = 200 2 V = U 0 ⇒ ϕ u = 0
+ Ở thời điểm t + 1 600 ( s ) = t + T 12 : ϕ u ' = ϕ u + π 6 = π 6
Lại có i = 0 và đang giảm ⇒ ϕ i ' = π 2 ⇒ φ = ϕ u ' − ϕ i ' = − π 3
Có P A B = P A M + P M B ⇔ U I cos φ = I 2 R 1 + P X ⇔ P X = 120 ( W )

1. Áp dụng : (\(\frac{i}{Io}\)) +(\(\frac{i}{Io}\))2=1 ta có : (\(\frac{i1}{Io1}\))2+(\(\frac{u1}{Uo1}\))2=(\(\frac{i2}{Io2}\))2+(\(\frac{u2}{Uo2}\))2 → (\(\frac{\sqrt{2}}{Io}\))2+(\(\frac{60\sqrt{6}}{Uo}\))2 =(\(\frac{\sqrt{6}}{Io}\))2+(\(\frac{60\sqrt{2}}{Uo}\))2 rút gọn đk :Uo=Io\(\times\)60
→Io \(\times\)Zl =Io \(\times\)60 →ZL=60 →w=120\(\Pi\)→f=60.
2.R thay đổi để Pmax=200 →Pmax=200=\(\frac{^{U2}}{2R}\)→ R=100. Mà R=|ZL-ZC| =100→ZC=200 →C=\(\frac{5\times10^{-5}}{\Pi}\)...ok