
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} \)\( = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)
Mà: \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)
\(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \) (do N là trung điểm của CD)
\( \Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)
b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0 \)
Từ ý a ta suy ra \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Ta có: \(\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG} \)
\( \Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Suy ra A, G, E thẳng hàng và \(AG = \frac{3}{4}AE \) nên G thuộc đoạn AE.

Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành.
Do đó: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AE} \).
Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\)
\( \Rightarrow \overrightarrow {AE} = \frac{1}{2}\overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Vậy \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Chú ý khi giải
+) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

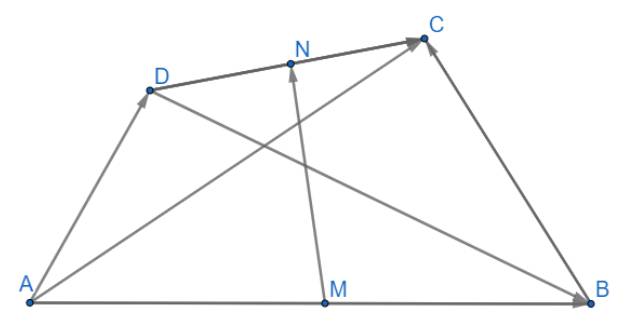
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)

Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)

1.
Dựng \(\overrightarrow{DB'}=\overrightarrow{CB}\)
\(k\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{DB}\)
\(=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{DA}+\overrightarrow{AB}\)
\(=2\overrightarrow{AB}+\overrightarrow{B'D}+\overrightarrow{DA}\)
\(=2\overrightarrow{AB}+\overrightarrow{B'A}\)
\(=2\overrightarrow{AB}+2\overrightarrow{AB}=4\overrightarrow{AB}\)
\(\Rightarrow k=4\)
Gọi M là trung điểm IB
\(\left|\overrightarrow{AB}+\overrightarrow{AI}\right|=\left|2\overrightarrow{AM}\right|=2AM\)
Ta có \(\overrightarrow{AM}^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2=MI^2+IA^2-2MI.IA.cos90^o=\dfrac{1}{16}a^2+\dfrac{3}{4}a^2=\dfrac{13}{16}a^2\)
\(\Rightarrow AM=\dfrac{\sqrt{13}}{4}a\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AI}\right|=\dfrac{\sqrt{13}}{2}a\)