Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

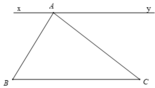
a) Có xy // BC (có hai góc so le trong bằng nhau), mà d // BC nên theo tiên đề Ơ-clit suy ra xy trùng với BC.
b) xy có thể trùng với d hoặc không ( xy trùng với d khi Δ A B C có A B C ^ = A C B ^ )

Giải
d1 và d2 là 2 đường thẳng trùng nhau vì:
+ Có một và chỉ một đường thẳng phân biệt vs đường thẳng đó
+ Có vô số đường thẳng trùng nhau song song với đường thẳng đó

a, Xét ∆ABC vuông tại A có: B + C = 90o
=> 30o + C = 90o
=> C = 60o
b, Vì CD là tia phân giác của C
=> ACD = DCB = ACB/2 = 60o/2 = 30o
Xét ∆ACB và ∆MCD
Có: AD: cạnh chung (gt)
ACD = DCM (vì CD là tia p/g của C)
CA = CM (gt)
=> ∆ACB = ∆MCD (c.g.c)
c, XY vuông góc CA => KCA = 90o
Vì AK // CD => CKA = CDA (2 góc so le trong)
Xét ∆CAK vuông tại C và ∆ADC vuông tại A
Có: CA: cạnh chung
CKA = CDA (cmt)
=> ∆CAK = ∆ADC (cgv-gn)
=> AK = DC (2 cạnh tương ứng)
d, Vì ∆CAK = ∆ADC (câu c)
=> KAC = ACD (2 góc tương ứng)
Mà ACD = 30o
=> KAC = 30o
Xét ∆KAC vuông tại C có: KAC + AKC = 90o
=> 30o + AKC = 90o
=> AKC = 60o