Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

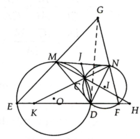
a, Ta có: D M N ^ = E ^ = G M N ^ , D N M ^ = N F D ^ = G N M ^
=> ∆GMN = ∆DMN
b, Chứng minh được MN là đường trung trực của GD
=> GD ⊥ EF (1)
Gọi J là giao điểm của DC và MN
Ta có J M D H = J N D K C J C D
Mặt khác: JM = JN (cùng bằng J C . J D )
=> DH = DK (2). Từ (1) và (2) Þ ĐPCM

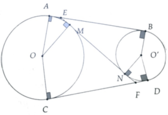
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF

a: TH1: A và CD nằm cùng một phía so với đường O'O
góc ABC=góc AEC=góc ICD
góc DBC=gsoc AED=góc IDC
=>góc DBA+góc DIC=góc ABC+góc DBC+góc DIC
=góc ICD+góc IDC+góc DIC=180 độ
=>BCID nội tiếp
TH2: A và CD nằm khác phía so với O'O
ABCE nội tiếp (O)
=>góc BCE+góc BAE=180 độ
=>góc BCE=góc BAF
Tương tự, ta được: góc BAF=góc BDI
=>góc BCE=góc BDI
=>góc BCI+góc BDI=180 độ
=>BCID nội tiếp
b: góc ICD=góc CEA=góc DCA
=>góc ICD=góc DCA
Chứng minh tương tự, ta được: góc IDC=góc CDA
Xét ΔICD và ΔACD có
góc ICD=góc DCA
CD chung
góc IDC=góc CDA
=>ΔICD=ΔACD
=>DI=DA và CI=CA
=>CD là trung trực của AI
c:
CD vuông góc AI
=>AI vuông góc MN
Gọi K là giao của AB và CD
Chứng minh được CK^2=KA*KB=KD^2
=>KC=KC
CD//MN
=>KC/AN=KD/AM=KB/AB
=>AN=AM
=>ΔIMN cân tại I
=>IA là phân giác của góc MIN