Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

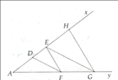
a: Xét ΔAEC có BD//EC
nên \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\)(1)
Xét ΔAEF có DC//EF
nên \(\dfrac{AC}{AF}=\dfrac{AD}{AE}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AB}{AC}=\dfrac{AC}{AF}\)
=>\(AC^2=AB\cdot AF\)

a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF

a/CE//BD, CB//EF theo Thales ta có
\(\frac{AB}{AC}=\frac{AD}{AE}\left(1\right),\frac{AC}{AF}=\frac{AD}{AE}\left(2\right)\)
b/(1) và (2) suy ra \(\frac{AB}{AC}=\frac{AC}{AF}\Rightarrow AC^2=AB.AF\)

a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF

Ta có: CE // BD, theo định lí Talet, ta được: \(\frac{AB}{AC}=\frac{AD}{AE}\left(1\right)\)
Lại có: CB // CF, theo định lí Talet, ta được: \(\frac{AC}{AF}=\frac{AD}{AE}\left(2\right)\)
Từ (1) và (2) ⇒ \(\frac{AB}{AC}=\frac{AC}{AF}\left(đpcm\right)\)