Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Năm số hạng đầu của dãy số
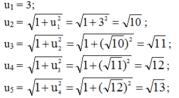
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
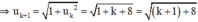
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

u1=-1
u2=-1+3=2
u3=2+3=5
u4=5+3=8
u5=8+3=11
Công thức tổng quát là: \(U_n=U_1+\left(n-1\right)\cdot\left(3\right)=-1+3n-3=3n-4\)

a. 5 số hạng đầu dãy là:
u1 = 2;
u2 = 2u1 – 1 = 3;
u3 = 2u2 – 1 = 5;
u4 = 2u3 – 1 = 9;
u5 = 2u4 – 1 = 17
b. Chứng minh un = 2n – 1 + 1 (1)
+ Với n = 1 ⇒ u1 = 21 - 1 + 1 = 2 (đúng).
+ Giả sử (1) đúng với n = k ≥ 1, tức là uk = 2k-1 + 1 (1)
Ta chứng minh: uk+1 = 2k + 1. Thật vậy, ta có:
⇒ uk+1 = 2.uk – 1 = 2(2k-1 + 1) – 1 = 2.2k – 1 + 2 – 1 = 2k + 1
⇒ (1) cũng đúng với n = k + 1 .
Vậy un = 2n – 1 + 1 với mọi n ∈ N.

Đặt \(u_n=v_n+1\Rightarrow v_{n+1}+1=\dfrac{2017+v_n+1}{2019-\left(v_n+1\right)}=\dfrac{2018+v_n}{2018-v_n}\)
\(\Rightarrow v_{n+1}=\dfrac{2018+v_n}{2018-v_n}-1=\dfrac{2v_n}{2018-v_n}\Rightarrow\dfrac{1}{v_{n+1}}=1009\dfrac{1}{v_n}-\dfrac{1}{2}\)
Đặt \(\dfrac{1}{v_n}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{1}{v_1}=\dfrac{1}{u_1-1}=1\\x_{n+1}=1009x_n-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x_{n+1}-\dfrac{1}{2016}=1009\left(x_n-\dfrac{1}{2016}\right)\)
\(\Rightarrow x_n-\dfrac{1}{2016}\) là CSN với công bội 1009 \(\Rightarrow x_n-\dfrac{1}{2016}=\dfrac{2015}{2016}.1009^{n-1}\)
\(\Rightarrow x_n=\dfrac{2015}{2016}1009^{n-1}+\dfrac{1}{2016}\)
\(\Rightarrow u_n=v_n+1=\dfrac{1}{x_n}+1=\dfrac{2016}{2015.1009^{n-1}+1}+1\)
\(\Rightarrow\lim\left(u_n\right)=1\)
Có thể đặt \(u_n=v_n+2017\) nữa bác nhỉ, bác có công thức tổng quát tìm t không ạ: \(u_n=v_n+t\).

Ta có:
u 2 = u 1 + 2 = 3 + 2 = 5.
u 3 = u 2 + 2 = 5 + 2 = 7.
u 4 = u 3 + 2 = 7 + 2 = 9.
u 5 = u 4 + 2 = 9 + 2 = 11.
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát u n có dạng:
u n = 2 n + 1 ∀ n ≥ 1 ∗
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.
Với n =1 ; u 1 = 2 . 1 + 1 = 3 (đúng). Vậy (*) đúng với n =1
Giả sử (*) đúng với n =k. Có nghĩa ta có: u k = 2 k + 1 (2)
Ta cần chứng minh (*) đúng với n = k+1 - có nghĩa là ta phải chứng minh:
u k + 1 = 2(k+1)+1= 2k + 3
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = u k +2 = 2k +1 +2 = 2k + 3
Vậy (*) đúng khi n = k+1 .
Kết luận (*) đúng với mọi số nguyên dương n.
Đáp án B

a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.

\(u_{n+1}=\sqrt{1+u_n^2}\left(1\right)\)
\(u_1=3=\sqrt{9}\)
\(u_2=\sqrt{1+u_1^2}=\sqrt{10}\)
\(u_3=\sqrt{1+u_2^2}=\sqrt{11}\)
...
Dự đoán công thức:\(u_n=\sqrt{n+8}\),\(n\ge1\) (*)
Thật vậy
+)\(n=1,(*)\)\(\Leftrightarrow u_1=3\) (lđ)
+)Giả sử (*) đúng với mọi \(n=k,k>1\)
\((*)\Leftrightarrow u_k=\sqrt{k+8}\)
+)\(n=k+1,\) thay vào (1) có: \(u_{k+2}=\sqrt{1+u^2_{k+1}}=\sqrt{1+\left(\sqrt{1+u_k^2}\right)^2}=\sqrt{2+u^2_k}=\sqrt{2+k+8}=\sqrt{10+k}\)
\(\Rightarrow\)(*) đúng với n=k+1
Vậy CTSHTQ: \(u_n=\sqrt{n+8}\), \(n\ge1\)

\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}+\dfrac{2}{n+2}\right)\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{n+1+1}=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}\right)\)
Đặt \(u_n-\dfrac{3}{n+1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{3}{2}=-\dfrac{1}{2}\\v_{n+1}=\dfrac{3}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\dfrac{3}{2}\)
\(\Rightarrow v_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}\)
\(\Rightarrow u_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}+\dfrac{3}{n+1}\)
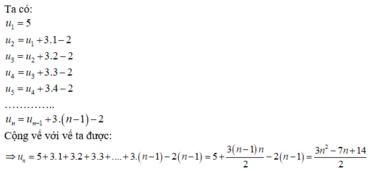
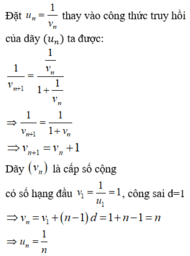
\(u_n=1+2\left(n-1\right)=1+2n-2=2n-1\left(\text{*}\right)\)
Chứng minh
Với \(n=1\)
\(VT=1;VP=2\cdot1-1=1=VT\)
Vậy \(\left(\text{*}\right)\) đúng với \(n=1\)
Giả sử \(\left(\text{*}\right)\) đúng với \(n=k\ge1\) tức là
\(u_k=u_{k-1}+2=2k-1\)
Ta chứng minh \(\left(\text{*}\right)\) đúng với \(n=k+1\)
Thật vậy, từ giả thuyết quy nạp ta có
\(u_{k+1}=u_k+2=2k-1+2=2k+2-1=2\left(k+1\right)-1\)
Vậy ...
Mới vô tính đú luôn toán lp 11 ak....đỉnh nhỉ...> . <...