Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
a) \(\sqrt{2x-4}\) có nghĩa khi:
\(2x-4\ge0\)
\(\Leftrightarrow2x\ge4\)
\(\Leftrightarrow x\ge\dfrac{4}{2}\)
\(\Leftrightarrow x\ge2\)
b) \(\sqrt{\dfrac{-7}{4-x}}\) có nghĩa khi
\(\dfrac{-7}{4-x}\ge0\) mà \(-7< 0\)
\(\Rightarrow4-x\le0\)
\(\Leftrightarrow x\ge4\)

Bài 1:
Ta có: \(\left(3\sqrt{50}-5\sqrt{18}+3\sqrt{8}\right)\cdot\sqrt{2}\)
\(=\left(15\sqrt{2}-15\sqrt{2}+6\sqrt{2}\right)\cdot\sqrt{2}\)
\(=6\sqrt{2}\cdot\sqrt{2}\)
=12
Bài 2:
1) ĐKXĐ: \(x\le0\)
2) ĐKXĐ: \(x\le2\)
3) ĐKXĐ: \(x>\dfrac{-3}{2}\)
4) ĐKXĐ: x>0
5) ĐKXĐ: x<3

bài 1:
a: Ta có: \(2\sqrt{18}-9\sqrt{50}+3\sqrt{8}\)
\(=6\sqrt{2}-45\sqrt{2}+6\sqrt{2}\)
\(=-33\sqrt{2}\)
b: Ta có: \(\left(\sqrt{7}-\sqrt{3}\right)^2+7\sqrt{84}\)
\(=10-2\sqrt{21}+14\sqrt{21}\)
\(=12\sqrt{21}+10\)
Bài 2:
a: Ta có: \(\sqrt{\left(2x+3\right)^2}=8\)
\(\Leftrightarrow\left|2x+3\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=8\\2x+3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)
b: Ta có: \(\sqrt{9x}-7\sqrt{x}=8-6\sqrt{x}\)
\(\Leftrightarrow4\sqrt{x}=8\)
hay x=4
c: Ta có: \(\sqrt{9x-9}+1=13\)
\(\Leftrightarrow3\sqrt{x-1}=12\)
\(\Leftrightarrow x-1=16\)
hay x=17

6:ĐKXĐ: x>=0; x<>1/25
BPT=>\(\dfrac{3\sqrt{x}}{5\sqrt{x}-1}+3< =0\)
=>\(\dfrac{3\sqrt{x}+15\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{18\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{1}{5}< \sqrt{x}< =\dfrac{5}{18}\)
=>\(\dfrac{1}{25}< x< =\dfrac{25}{324}\)
7:
ĐKXĐ: x>=0
BPT \(\Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}>\dfrac{8}{3}:\dfrac{8}{3}=1\)
=>\(\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}-1>=0\)
=>\(\dfrac{\sqrt{x}+1-2\sqrt{x}-3}{2\sqrt{x}+3}>=0\)
=>\(-\sqrt{x}-2>=0\)(vô lý)
8:
ĐKXĐ: x>=0; x<>9/4
BPT \(\Leftrightarrow\dfrac{\sqrt{x}-2}{2\sqrt{x}-3}+4< 0\)
=>\(\dfrac{\sqrt{x}-2+8\sqrt{x}-12}{2\sqrt{x}-3}< 0\)
=>\(\dfrac{9\sqrt{x}-14}{2\sqrt{x}-3}< 0\)
TH1: 9căn x-14>0 và 2căn x-3<0
=>căn x>14/9 và căn x<3/2
=>14/9<căn x<3/2
=>196/81<x<9/4
TH2: 9căn x-14<0 và 2căn x-3>0
=>căn x>3/2 hoặc căn x<14/9
mà 3/2<14/9
nên trường hợp này Loại
9:
ĐKXĐ: x>=0
\(BPT\Leftrightarrow\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}< =-\dfrac{1}{3}\)
=>\(\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}+\dfrac{1}{3}< =0\)
=>\(\dfrac{6\sqrt{x}+9+5\sqrt{x}+7}{3\left(5\sqrt{x}+7\right)}< =0\)
=>\(\dfrac{11\sqrt{x}+16}{3\left(5\sqrt{x}+7\right)}< =0\)(vô lý)
10:
ĐKXĐ: x>=0; x<>1/49
\(BPT\Leftrightarrow\dfrac{6\sqrt{x}-2}{7\sqrt{x}-1}+6>0\)
=>\(\dfrac{6\sqrt{x}-2+42\sqrt{x}-6}{7\sqrt{x}-1}>0\)
=>\(\dfrac{48\sqrt{x}-8}{7\sqrt{x}-1}>0\)
=>\(\dfrac{6\sqrt{x}-1}{7\sqrt{x}-1}>0\)
TH1: 6căn x-1>0 và 7căn x-1>0
=>căn x>1/6 và căn x>1/7
=>căn x>1/6
=>x>1/36
TH2: 6căn x-1<0 và 7căn x-1<0
=>căn x<1/6 và căn x<1/7
=>căn x<1/7
=>0<=x<1/49

đk : \(x\ge0,x\ne1\)
\(=>P=\left[\dfrac{2\left(\sqrt{x}+2\right)-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right]:\left[\dfrac{x+\sqrt{x}-2+3-x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right]\)
\(P=\left[\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right].\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+1}\right]\)
\(P=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
b,\(x=6-2\sqrt{5}=\left(\sqrt{5}-1\right)^2\) thay vào P
\(=>P=\dfrac{2\sqrt{\left(\sqrt{5}-1\right)^2}-1}{\sqrt{\left(\sqrt{5}-1\right)^2}+1}=\dfrac{2\sqrt{5}-3}{\sqrt{5}}\)
c,\(=>\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}}=>2x-\sqrt{x}=\sqrt{x}+1\)
\(=>2x-2\sqrt{x}-1=0< =>2\left(x-\sqrt{x}-\dfrac{1}{2}\right)=0\)
\(=>x-\sqrt{x}-\dfrac{1}{2}=>\Delta=1-4\left(-\dfrac{1}{2}\right)=3>0=>\left[{}\begin{matrix}x1=\dfrac{1+\sqrt{3}}{2}\\x2=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\)
đối chiếu đk loại x2 còn x1 thỏa

a) \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{x-1}=\dfrac{1}{x-1}\)

b: Ta có: \(B=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\left(\dfrac{x\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x+\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\left(x+\sqrt{x}+1+\sqrt{x}\right)\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}-1}\)

Câu 2:
a, ĐKXĐ: x\(\ge\)0; x\(\ne\)\(\pm\)1
B=
\(\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ =\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ =\dfrac{-2.2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ =\dfrac{-4\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ =\dfrac{4\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ =-\dfrac{4}{\sqrt{x}-1}\)

`a)sqrt{28a^4}`
`=sqrt{7.4.a^4}`
`=2sqrt7a^2`
`b)A=((sqrt{21}-sqrt7)/(sqrt3-1)+(sqrt{10}-sqrt5)/(sqrt2-1)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt3-1))/(sqrt3-1)+(sqrt5(sqrt2-1))/(sqrt2-1)).(sqrt7-sqrt5)`
`=(sqrt7+sqrt5)(sqrt7-sqrt5)`
`=7-5=2`
`c)` $\begin{cases}\dfrac{3}{2x}-y=6\\\dfrac{1}{x}+2y=-4\end{cases}$
`<=>` $\begin{cases}\dfrac{3}{x}-2y=12\\\dfrac{1}{x}+2y=-4\end{cases}$
`<=>` $\begin{cases}\dfrac{4}{x}=8\\2y+\dfrac{1}{x}=-4\end{cases}$
`<=>` $\begin{cases}x=\dfrac12\\2y=-4-2=-6\end{cases}$
`<=>` $\begin{cases}x=\dfrac12\\y=-3\end{cases}$
Vậy HPT có nghiệm `(x,y)=(1/2,-3)`.
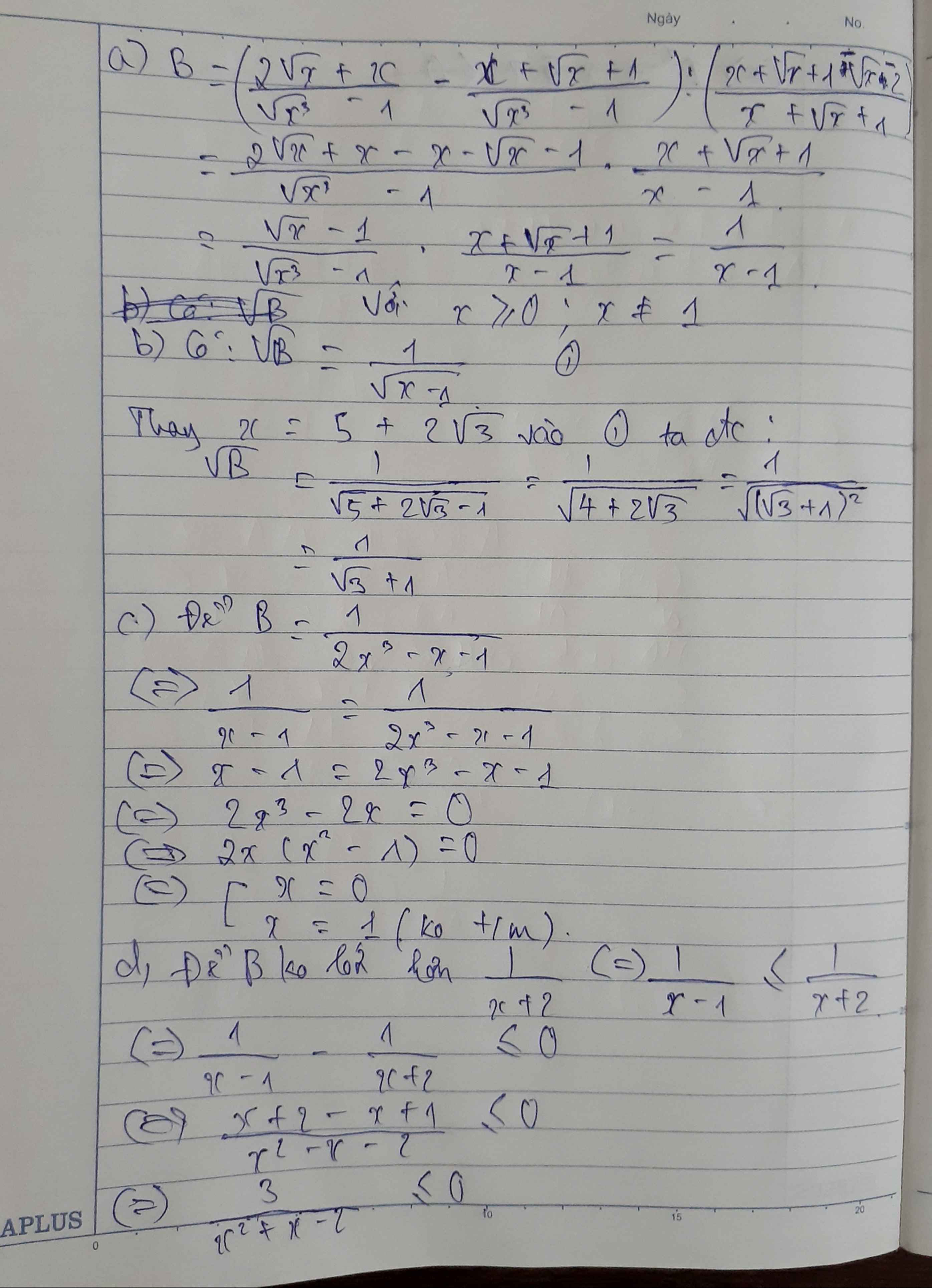
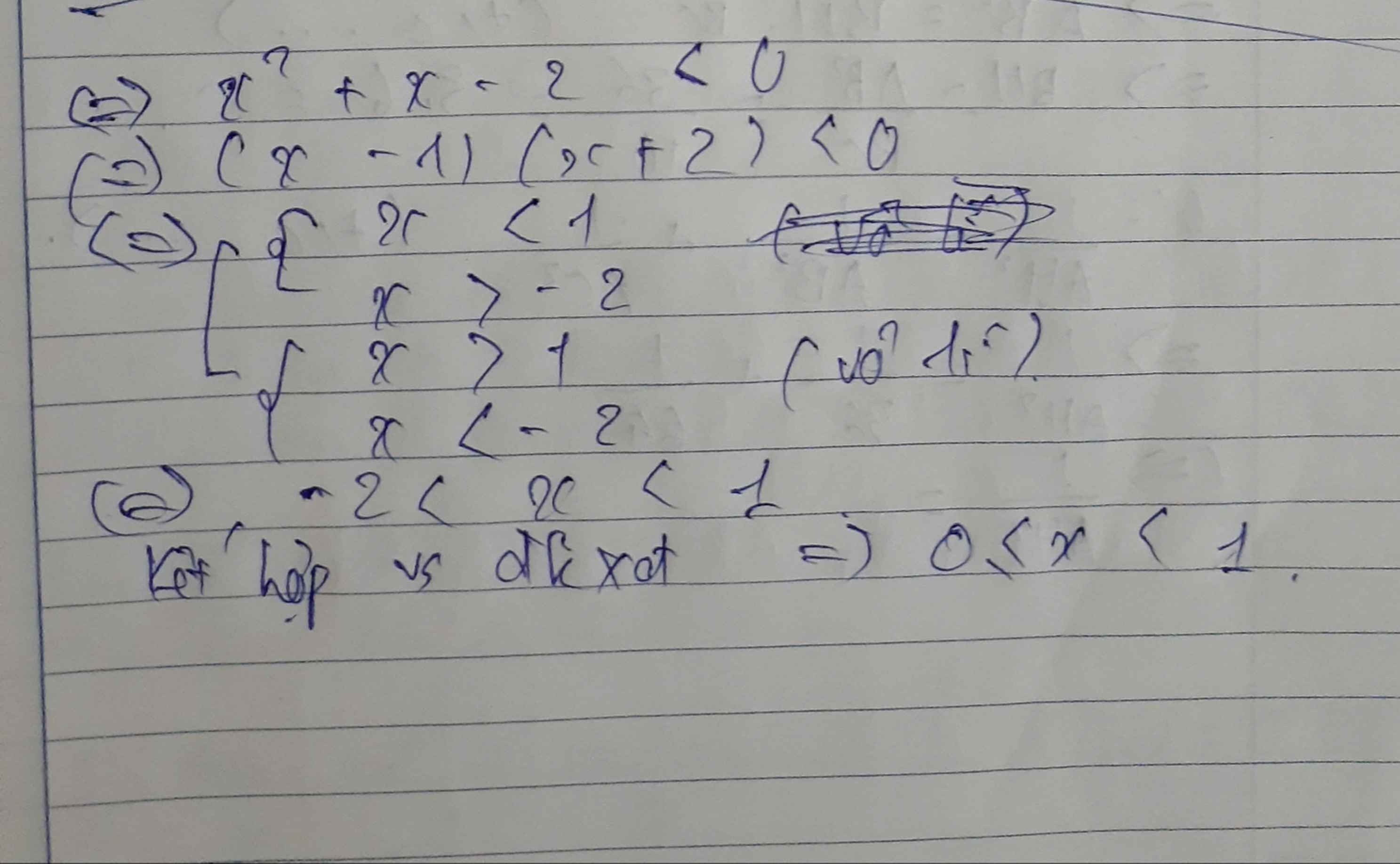
Bài 2:
a: Ta có: \(\sqrt{8-2\sqrt{15}}\cdot\left(\sqrt{60}+6\right):2\sqrt{3}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{12}\left(\sqrt{5}+\sqrt{3}\right):2\sqrt{3}\)
\(=2\sqrt{12}:2\sqrt{3}\)
=2
b: Ta có: \(\sqrt{5-\sqrt{21}}-\sqrt{\dfrac{7}{2}}\)
\(=\dfrac{\sqrt{10-2\sqrt{21}}-\sqrt{7}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{7}-\sqrt{3}-\sqrt{7}}{\sqrt{2}}\)
\(=-\dfrac{\sqrt{6}}{2}\)