Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: a:b=\(\frac{2}{7}\)=>a=\(\frac{2}{7}\)*b
Ta có:\(\frac{a+35}{b}\)=\(\frac{11}{14}\)
=>(a+35)*14=11b
=>14a+490=11b
=>14*\(\frac{2}{7}\)*b+490=11b
=>4b+490=11b
=>490=11b-4b
=>490=7b
=>b=490:7
=>b=70
=>a=70*\(\frac{2}{7}\)
=>a=20
Vậy a=20;b=70(Đề là thêm 35 đơn vị vào a;còn lại giữ nguyên)

Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x_A=\dfrac{-2}{2\cdot1}=-1\\y_A=\dfrac{-\left(2^2-4\cdot1\cdot\left(-2\right)\right)}{4}=\dfrac{-\left(4+8\right)}{4}=-3\end{matrix}\right.\)
A(-1;-3)
Vì a=1>0 nên hàm số đồng biến trên khoảng (-1;+\(\infty\)), nghịch biến trên khoảng (-\(\infty\);-1)

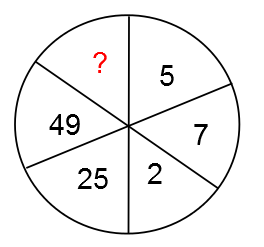
Theo đề bài ta nhận thấy số đối diện số 5 là số 25
=> Quy luật là : n2
=> 52 = 25
=> 72 = 49
<=> 22 = 4

mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)

Mình giải được phần 1 rồi nhưng không biết cách viết bài giải để gửi cho bn :))), theo mình thì phần 1 bạn chuyển căn thứ nhất với căn thứ 3 thành 1 cặp, căn thứ hai với căn thứ tư thành một cặp sau đó nhân liên hợp nhé!