Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đổi \(20cm=0,2m\)
\(=>PA=PB\)
\(=>dd.h1=dn.h2\)
\(< =>8000h1=10000\left(h1-0,2\right)=>h1=1m\)

Để giải bài toán này, chúng ta sẽ áp dụng các nguyên tắc về áp suất trong chất lỏng và các công thức về áp suất thủy tĩnh. Ta sẽ làm lần lượt từng phần của bài toán.
### a) Tính độ chênh lệch mực nước trong 2 nhánh
1. **Áp suất do cột dầu trong nhánh nhỏ:**
- Chiều cao cột dầu \( h = 10 \) cm = 0.1 m.
- Khối lượng riêng của dầu \( D_2 = 800 \) kg/m³.
- Áp suất do cột dầu gây ra ở đáy nhánh nhỏ:
\[
P_dầu = D_2 \cdot g \cdot h = 800 \cdot 9.81 \cdot 0.1 = 784.8 \, \text{Pa}
\]
2. **Áp suất này sẽ đẩy nước từ nhánh nhỏ sang nhánh lớn, tạo ra một độ chênh lệch mực nước:**
- Gọi độ chênh lệch mực nước trong hai nhánh là \( \Delta h \).
- Áp suất do cột nước chênh lệch này phải bằng áp suất do cột dầu, vì hai nhánh thông nhau và mức chất lỏng cân bằng ở đáy:
\[
D_1 \cdot g \cdot \Delta h = P_dầu
\]
\[
1000 \cdot 9.81 \cdot \Delta h = 784.8
\]
\[
\Delta h = \frac{784.8}{1000 \cdot 9.81} = 0.08 \, \text{m} = 8 \, \text{cm}
\]
3. **Mực nước ở nhánh lớn và nhánh nhỏ:**
- Mực nước ở nhánh lớn dâng lên một nửa độ chênh lệch này do diện tích nhánh lớn gấp đôi diện tích nhánh nhỏ:
\[
h_\text{dâng lên, nhánh lớn} = \frac{\Delta h}{2} = \frac{8}{2} = 4 \, \text{cm}
\]
- Mực nước ở nhánh nhỏ hạ xuống tương ứng:
\[
h_\text{hạ xuống, nhánh nhỏ} = 4 \, \text{cm}
\]
### b) Đặt một piston có khối lượng lên nhánh lớn để mực nước cân bằng
1. **Để mực nước trong 2 nhánh bằng nhau:**
- Ta cần tạo ra áp suất thêm vào nhánh lớn để cân bằng áp suất do cột dầu trong nhánh nhỏ.
2. **Áp suất cần thêm vào nhánh lớn để cân bằng:**
- Ta phải đẩy nhánh lớn xuống một khoảng \( \Delta h = 8 \, \text{cm} \).
3. **Tính lực cần thêm vào nhánh lớn:**
- Diện tích nhánh lớn \( A_\text{lớn} = 100 \, \text{cm}^2 = 0.01 \, \text{m}^2 \).
- Áp suất thêm vào nhánh lớn để cân bằng áp suất do cột dầu:
\[
P_\text{piston} = D_1 \cdot g \cdot \Delta h = 1000 \cdot 9.81 \cdot 0.08 = 784.8 \, \text{Pa}
\]
4. **Tính khối lượng của piston:**
- Áp suất là lực trên diện tích, do đó:
\[
P_\text{piston} = \frac{F}{A_\text{lớn}}
\]
\[
F = P_\text{piston} \cdot A_\text{lớn} = 784.8 \cdot 0.01 = 7.848 \, \text{N}
\]
- Khối lượng của piston:
\[
m = \frac{F}{g} = \frac{7.848}{9.81} \approx 0.8 \, \text{kg}
\]
Vậy:
a) Độ chênh lệch mực nước trong hai nhánh là 8 cm. Mực nước nhánh lớn dâng lên 4 cm và mực nước nhánh nhỏ hạ xuống 4 cm.
b) Để mực nước trong hai nhánh bằng nhau, cần đặt một piston có khối lượng khoảng 0.8 kg lên nhánh lớn.

Câu a:
Gọi độ chênh lệch mực nc là h.
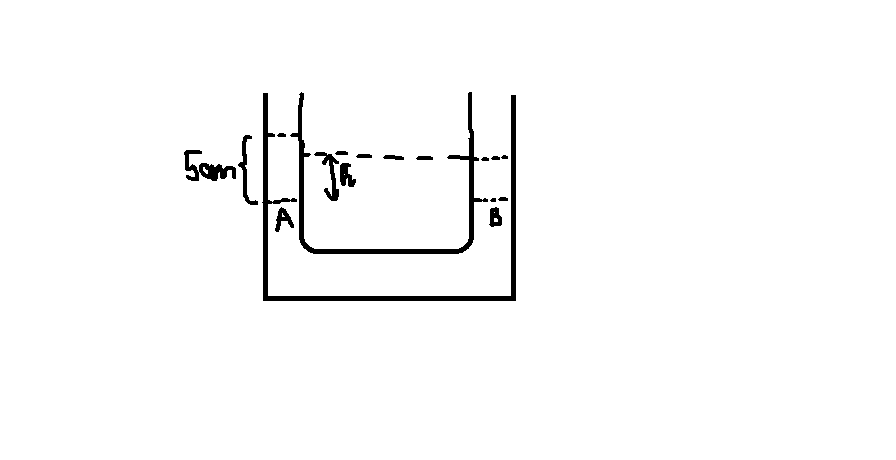
\(p_A=8000\cdot0,05=400Pa\)
\(p_B=d_n\cdot h=10000h\left(Pa\right)\)
Tại hai điểm A,B: \(p_A=p_B\)
\(\Rightarrow400=10000h\Rightarrow h=0,04m=4cm\)

Gọi diện tích tiết diện của ống nhỏ là S, thì diện tích tiết diện của ống lớn là 2S. Sau khi mở khóa T, cột nước ở 2 nhánh có cùng chiều cao h.
Do thể tích nước trong bình thông nhau trước và sau khi mở khóa K là không đổi nên ta có: Vtrước = Vsau ↔ H.2S = h.S + 2S.h
(H là chiều cao cột nước lúc đầu khi chưa mở khóa K)
⇒ 2.H = h + 2.h ⇒ h = 20cm.

Bình thông nhau có hai nhánh A và B.
\(\Rightarrow\)Áp suất tại hai điểm M, N của hai nhánh đó cũng bằng nhau.\(\Rightarrow p_M=p_N\)
\(\Rightarrow d_{nc}\cdot g\cdot h_M=d_{dầu}g\cdot h_N\Rightarrow1\cdot h_M=0,8\cdot20\)
\(\Rightarrow h_M=16cm\)
Độ chênh lệch mực chất lỏng:
\(\Delta h=20-16=4cm\)

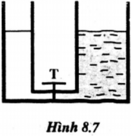
- Gọi diện tích tiết diện của ống nhỏ là s, ống lớn là 2s.
- Sau khi mở khóa T cột nước ở hai nhánh có cùng chiều cao h.
- Do thể tích nước trong bình thông nhau là không đổi nên ta có:
2s.30 = s.h + 2s.h
⇒ h = 20 cm
⇒ Đáp án B
a) Khi mở khóa, nước sẽ chảy tự do giữa hai nhánh của bình. Ta có thể áp dụng nguyên lý Pascal để tính chiều cao cột nước trong mỗi nhánh sau khi mở khóa.
Áp suất nước trong bình là như nhau, vì vậy ta có: P1 = P2
Với S1 là diện tích đáy nhánh 1 và h1 là chiều cao cột nước trong nhánh 1, ta có: P1 = ρgh1S1
Tương tự, với S2 là diện tích đáy nhánh 2 và h2 là chiều cao cột nước trong nhánh 2, ta có: P2 = ρgh2S2
Vì P1 = P2, ta có: ρgh1S1 = ρgh2S2
Từ đó, ta có: h1S1 = h2S2
Tính chiều cao cọt nước mỗi nhánh sau khi mở khóa:
Vậy, chiều cao cọt nước trong nhánh 1 sau khi mở khóa là 45cm và trong nhánh 2 là 13.33cm.
b) Vật đặc không thấm nước được thả vào nhánh lớn. Ta cần tính chiều cao vật chìm và chiều cao nước dâng mỗi nhánh.
Vật chìm hoàn toàn trong nước, nên thể tích của vật bằng thể tích nước đã chuyển đi.
Thể tích vật = Thể tích nước dâng trong nhánh lớn
=> a^3 = S1 * h1
=> 6cm^3 = 80cm^2 * h1
=> h1 = 6cm^3 / 80cm^2 = 0.075cm (làm tròn thành 3 chữ số thập phân)
Chiều cao nước dâng trong mỗi nhánh là chiều cao cột nước ban đầu trừ đi chiều cao vật chìm:
Vậy, chiều cao vật chìm là 0.075cm, chiều cao nước dâng trong nhánh 1 là 19.925cm và trong nhánh 2 là 29.925cm.
c) Để tính khối lượng dầu đổ vào, ta cần tính thể tích dầu.
Thể tích dầu = Thể tích không gian giữa mặt trên vật và mặt trên dầu
= S1 * 0.02m (do mặt trên dầu cách mặt trên vật 2cm)
= 80cm^2 * 0.02m = 1.6cm^3
Khối lượng dầu = Thể tích dầu * mật độ dầu
= 1.6cm^3 * 8000 N/m^3 = 12800 N
Vậy, khối lượng dầu đổ vào là 12800 N.