Khi cung cấp cho vật kl m1 vận tốc ban đầu v1 =4m/s thì nó sẽ trượt đc đoạn đường dài 2 m trên mặt phẳng nằm ngang rồi dừng lại do có ma sát .Nếu cung cấp vật kl m2 = 2m1 vận tốc ban đầu v2 = 6m/s để m2 cũng trượt trên mặt phẳng đó thì khi dừng lại m2 đã trượt đc đoạn đường bằng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2019
biến thiên động năng (v1'=0)
\(A_{F_{ms}}=\dfrac{1}{2}.m_1.\left(v_{1'}^2-v_1^2\right)\)
\(\Rightarrow F_{ms}.s.cos180^0=\)-8.m1
\(\Rightarrow F_{ms}=4m_1\)
đối với vật m2=2m1
biến thiên động năng(v2'=0)
\(A_{F_{ms}}=\dfrac{1}{2}.m_2.\left(v^2_{2'}-v^2_2\right)\)
\(\Leftrightarrow4m_1.s.cos180^0=m_1.\left(-36\right)\)
\(\Rightarrow s=\)9m
VT
9 tháng 5 2017
Đáp án: A
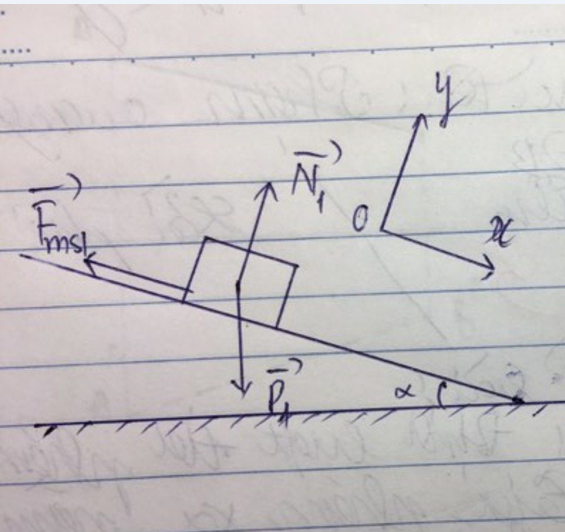
Phương trình động lực học:
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
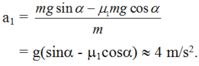
Vận tốc của vật tại B:
Gia tốc của vật trên mặt phẵng ngang:
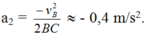
Trên mặt phẵng ngang ta có:
30 tháng 11 2021
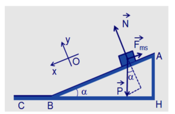
Hình vẽ bạn tham khảo.
Theo định luật ll Niu-tơn ta có:
\(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Oy: \(N=P=mg=10m\left(N\right)\)
\(Ox:\) \(-F_{ms}=m\cdot a\)
\(\Rightarrow-\mu mg=m\cdot a\Rightarrow a=-\mu\cdot g=-0,5\cdot10=-5\)m/s2
Quãng đường vật đi:
\(v^2-v^2_0=2aS\Rightarrow S=\dfrac{v^2-v^2_0}{2a}=\dfrac{0-12^2}{2\cdot\left(-5\right)}=14,4m\)
Chọn A.
VT
29 tháng 12 2018
Lực ma sát tác dụng lên vật là:
F m s = μ N = μ m g = 0 , 1. m .10 = m N
Sử dụng định luật II - Niutơn: : F → = m a →
F m s = F ↔ m a = m ( N ) → a = 1 m / s 2
Ta có:
v 2 − v 0 2 = 2 a s → s = v 0 2 2 a = 10 2 2 = 50 m
Đáp án: D
10 tháng 5 2021
Lực ma sát tác dụng lên vật là:
F m s = μ N = μ m g = 0 , 1. m .10 = m N
Sử dụng định luật II - Niutơn: : F → = m a →
F m s = F ↔ m a = m ( N ) → a = 1 m / s 2
Ta có:
v 2 − v 0 2 = 2 a s → s = v 0 2 2 a = 10 2 2 = 50 m
biến thiên động năng \(\left(v1=0\right)\)
\(A.F_{ms}=\frac{1}{2}.m1.\left(v\overset{2}{1'}-v\overset{2}{1}\right)\)
\(\Rightarrow F_{ms}.s.\cos180^o=-8.m1\)
\(\Rightarrow F_{ms}=4m1\)
đối với mật m2=2m1
biến thiên động năng (v2'=0)
\(A.F_{ms}=\frac{1}{2}.m2.\left(v\overset{2}{2'}-v\overset{2}{2}\right)\)
\(\Leftrightarrow4m1.s.\cos180^o=m1.\left(-36\right)\)
\(\Leftrightarrow s=9m\)
Khi cung cấp cho vật kl m1 vận tốc ban đầu v1 =4m/s thì nó sẽ trượt đc đoạn đường dài 2 m trên mặt phẳng nằm ngang rồi dừng lại do có ma sát .Nếu cung cấp vật kl m2 = 2m1 vận tốc ban đầu v2 = 6m/s để m2 cũng trượt trên mặt phẳng đó thì khi dừng lại m2 đã trượt đc đoạn đường bằng bao nhiêu
______________________________
Giải
Khi bắt đầu chuyển động đến khi dừng lại động năng của vật đã chuyển hóa thành công của lực ma sát
\(\left\{{}\begin{matrix}W_{d1}=A_{F_{ms1}}\\W_{d2}=A_{F_{ms2}}\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}\frac{1}{2}m_1v_1^2=\mu m_1g .s_1\\\frac{1}{2}m_2v_2^2=\mu.m_2\text{g }.s_1\end{matrix}\right.\)
\(\rightarrow s_1=s_2.\frac{v_2^2}{v_1^2}=2.\frac{6^2}{4^2}=4,5\left(m\right)\)