Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

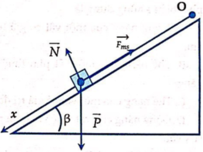
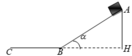
theo định luật II niu tơn trên mặt phẳng nghiêng AB
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng nằm nghiêng chiều dương cùng chiều chuyển động
\(sin\alpha.P-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng, chiều dương hướng lên trên
N=\(cos\alpha.P\) (3)
từ (2),(3)
\(\Rightarrow sin\alpha.g-\mu.g.cos\alpha=a\)
\(\Rightarrow a\approx4,1\)m/s2
vận tốc lúc vật tại B
\(v^2-v_0^2=2as_{AB}\Rightarrow v\approx2,875\)m/s

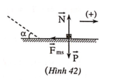
Định luật II Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Ox: \(Psin\alpha-F_{ms}=m\cdot a\)
Oy: \(N-Pcos\alpha=0\Rightarrow N=Pcos\alpha=mgcos\alpha\)
\(F_{ms}=\mu_1\cdot N=\mu_1\cdot mgcos\alpha\)
Gia tốc mặt phẳng nghiêng:
\(a=\dfrac{Psin\alpha-F_{ms}}{m}=\dfrac{mgsin\alpha-\mu_1mgcos\alpha}{m}=g\left(sin\alpha-\mu_1cos\alpha\right)=10\left(sin30-0,1cos30\right)\approx4,13\)m/s2


![]()
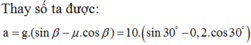
![]()
+ Theo công thức liên hệ a;v; S trong chuyển động thẳng biến đổi đều ta có:
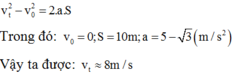

Chọn mốc thế năng tại mặt nằm ngang BC
Theo định luật bảo toàn năng lượng
W A = W C + A m s
Mà W A = m g . A H = m .10 = 10. m ( J ) ; W C = 0 ( J ) A m s = μ m g cos α . A B + μ m g . B C = 0 , 1. m .10. cos 30 0 . A H sin 30 0 + 0 , 1. m .10. B C ⇒ A m s = m . 3 . + m . B C ⇒ 10. m = 0 + m 3 + m . B C ⇒ B C = 8 , 268 ( m )

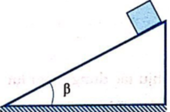
Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 8.10.0 , 5 = 4 ( N ) P 2 = m 2 g = 0 , 6.10 = 6 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 50 cm thì vật một lên cao
z 1 = s . sin 30 0 = s 2 = 25 ( c m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s V ớ i W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 8 + 0 , 6 ) .1 2 2 = 0 , 7 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = μ .0 , 8.10. 3 2 .0 , 5 = μ 2 3 ( J )
Vậy 0 = 0 , 7 − 1 + μ .2. 3 ⇒ μ = 0 , 0866
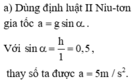

Đáp án: A
Phương trình động lực học:
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
Vận tốc của vật tại B:
Gia tốc của vật trên mặt phẵng ngang:
Trên mặt phẵng ngang ta có: