Cho tam giác ABC vuông tại A, đường cao AH. Biết AB: 12cm, AH:7,2 cm. tính AC BC BH CH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
1
H9
HT.Phong (9A5)
CTVHS
1 tháng 10 2023
Xét tam giác ABC vuông tại A ta có:
\(AB^2=BC\cdot BH\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{2}{3}\right)^2}{12}=\dfrac{1}{27}\left(cm\right)\)
Mà: \(BC=CH+BH\)
\(\Rightarrow CH=12-\dfrac{1}{27}=\dfrac{323}{27}\left(cm\right)\)
\(AC^2=BC\cdot CH\)
\(\Rightarrow AC=\sqrt{BC\cdot CH}=\sqrt{12\cdot\dfrac{323}{27}}=\dfrac{2\sqrt{323}}{3}\left(cm\right)\)
Mà: \(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{2}{3}\cdot\dfrac{2\sqrt{323}}{3}}{12}=\dfrac{\sqrt{323}}{27}\left(cm\right)\)
PQ
0
4 tháng 8 2016
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
HQ
0
AH
Akai Haruma
Giáo viên
22 tháng 5 2021
Lời giải:
1) Xét tam giác $BHA$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}$
$\Rightarrow BH=\frac{BA^2}{BC}=\frac{6^2}{8}=4,5$ (cm)
$CH=BC-BH=8-4,5=3,5$ (cm)
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{8^2-6^2}=2\sqrt{7}$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{6.2\sqrt{7}}{8}=\frac{3\sqrt{7}}{2}$ (cm)
2. 3. Những phần này bạn làm tương tự như phần 1.
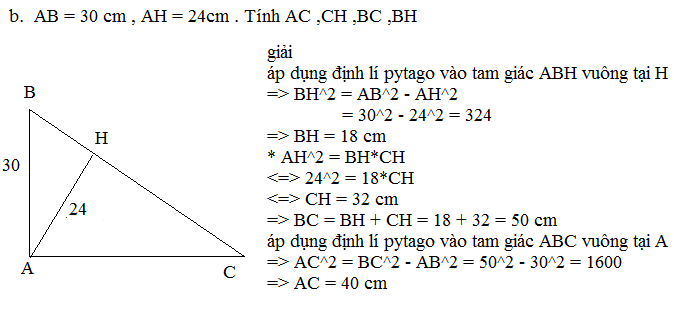
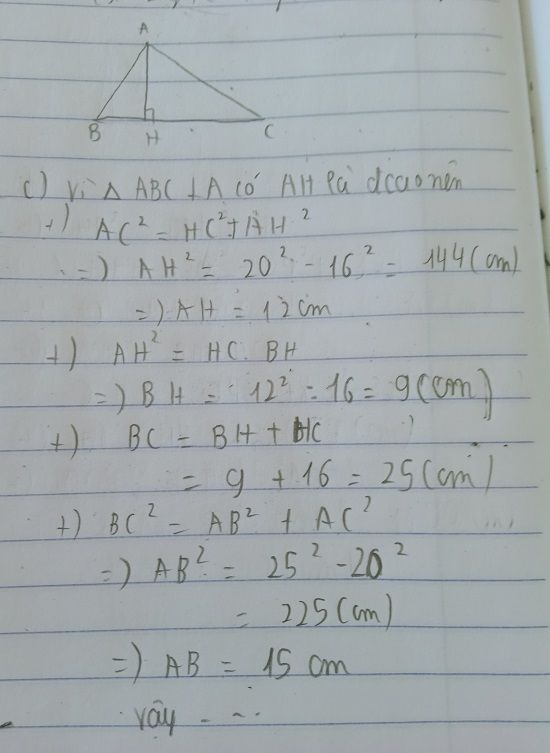
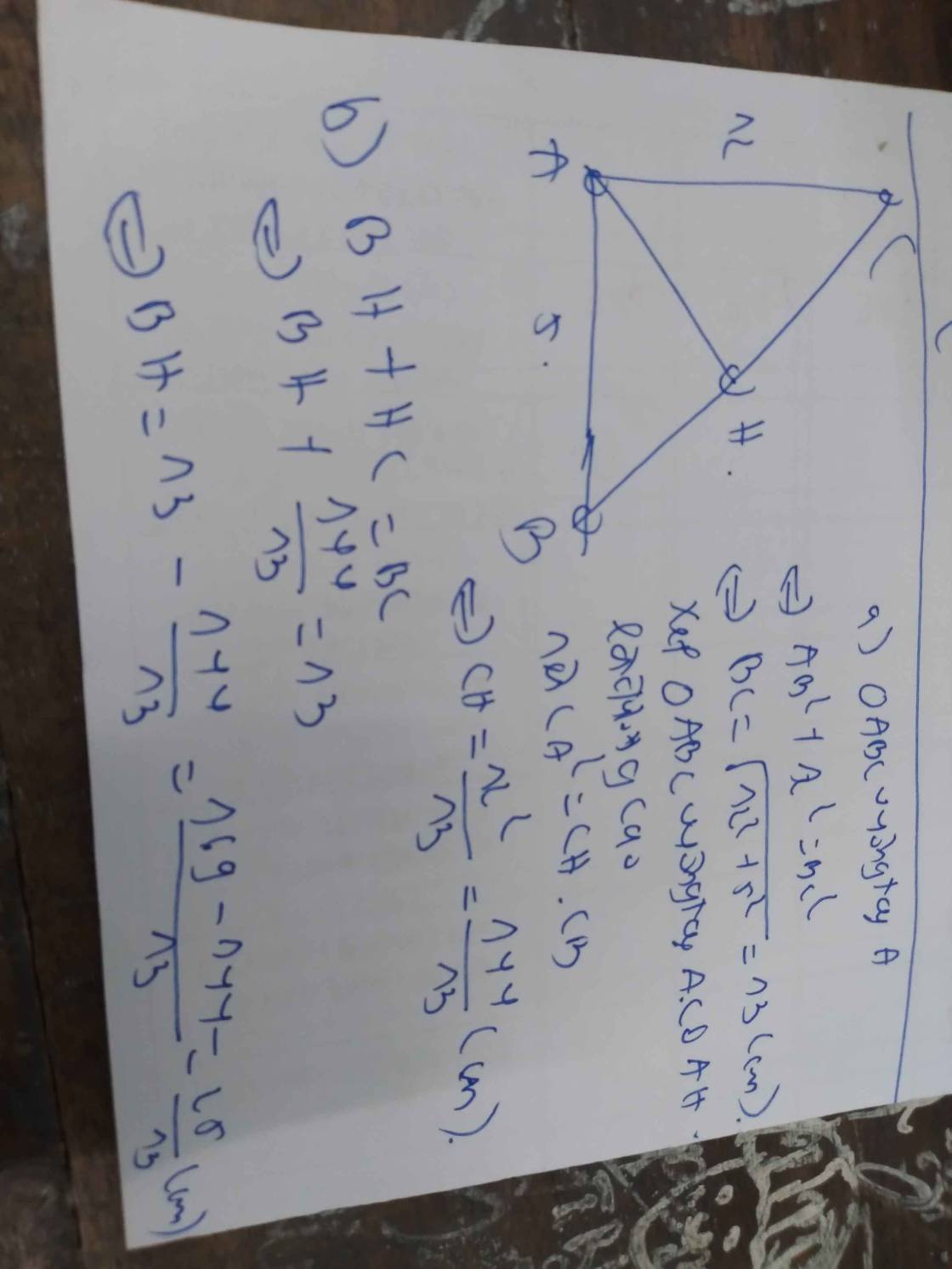
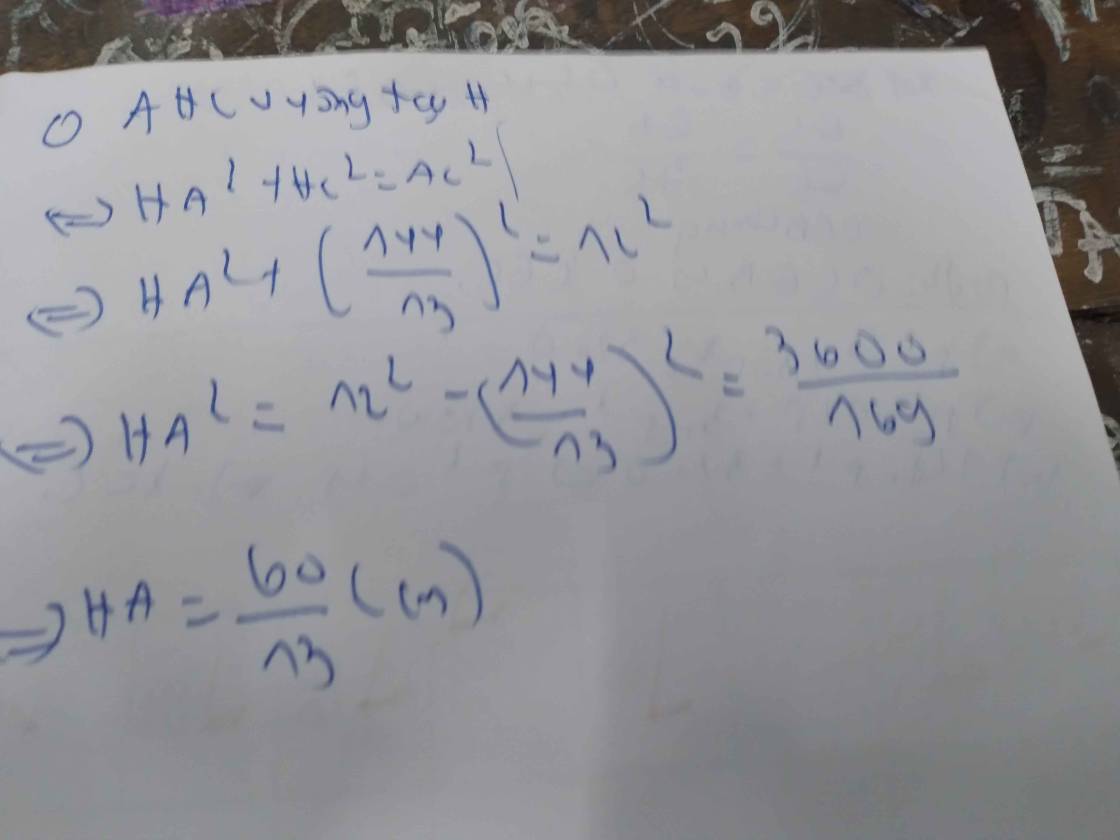
Áp dụng HTL:
\(\dfrac{1}{AH^2}=\dfrac{1}{51,84}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{144}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{AC^2}=\dfrac{1}{81}\Rightarrow AC=9\left(cm\right)\)
Áp dụng PTG \(BC=\sqrt{BA^2+AC^2}=15\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)