Cho tam giác nhọn ABC ( AB < AC ). Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy điểm M sao cho DM = DA
a) Chứng minh ΔACD = ΔMBD. Từ đó suy ra AC = BM, và AC // BM
b) Chứng minh ΔABM = ΔMCA
c) Kẻ AH ⊥ BC, MK ⊥ BC (H,K ∈ BC). Chứng minh BK = CH
d) Chứng minh HM // AK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 1 2022
a/ Xét tg ADB và tg MDC có
AD=DM (gt) DB=DC (gt)
\(\widehat{ADB}=\widehat{MDC}\)(góc đối đỉnh)
=> tg ADB = tg MDC (c.g.c) => AC=BM
\(\Rightarrow\widehat{CAD}=\widehat{BMD}\)=> AC // BM (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)
b/
Xét tg ABM và tg MCA có
tg ABD = tg MCD (cmt) => AB = MC; AC = BM
AM chung
=> tg ABM = tg MCA (c.c.c)
c/
Xét tg vuông ABH và tg vuông MCK có
tg ABD = tg MCD (cmt) => \(\widehat{ABH}=\widehat{MCK}\)
AB=CM (cmt)
=> tg ABH = tg MCK (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau) => BH=CK
Mà BK=BC-CK; CH=BC-BH => BK=CH
d/
Xét tg vuông AHD và tg vuông MKD có
DA=DM (gt); \(\widehat{ADH}=\widehat{MDK}\)(góc đối đỉnh) => tg AHD = tg MKD (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DMK}\) => HM // AK (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)
YN
11 tháng 7 2023
\(a,\)
Xét \(\triangle ADC\) và \(\triangle MDB\):
\(DA=DM\)
\(DC=DB\)
\(\widehat{ADC}=\widehat{MDB}\)
\(\Rightarrow\Delta ADC=\Delta MDB\left(c.g.c\right)\) \(\left(1\right)\)
\(\left(1\right)\Rightarrow AC=BM\)
\(\Rightarrow\widehat{ACD}=\widehat{MBD}\)
mà hai góc này nằm ở vị trí so le trong
\(\Rightarrow\)\(AC//BM\)
\(b,\)
\(\left(1\right)\Rightarrow\widehat{DAC}=\widehat{DMB}\)
Xét \(\triangle ABM\) và \(\triangle MCA\):
\(AM\) chung
\(BM=AC\)
\(\widehat{DAC}=\widehat{DMB}\)
\(\Rightarrow\Delta ABM=\Delta MCA\left(c.g.c\right)\).
11 tháng 7 2023
a: Xét tứ giác ABMC có
D là trung điểm chung của AM và BC
=>ABMC là hình bình hành
=>AC//BM và AC=BM
b: Xét ΔABM và ΔMCA có
AB=MC
BM=CA
AM chung
=>ΔABM=ΔMCA
16 tháng 2 2022
a) Xét tam giác ABD và tam giác ACD:
AD chung.
AB = AC (gt).
BD = CD (D là trung điểm của BC).
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-c-c\right).\)
b) Xét tam giác ABC: AB = AC (gt).
\(\Rightarrow\Delta ABC\) cân tại A.
Mà AD là trung tuyến (D là trung điểm của BC).
\(\Rightarrow\) AD là phân giác \(\widehat{BAC}\) (Tính chất tam giác cân).
Xét tam giác MAD và tam giác NAD:
AD chung.
AM = AN (gt).
\(\widehat{MAD}=\widehat{NAD}\) (AD là phân giác \(\widehat{BAC}\)).
\(\Rightarrow\Delta MAD=\Delta NAD\left(c-g-c\right).\)
\(\Rightarrow\) DM = DN (2 cạnh tương ứng).
c) Xét tam giác ADC và tam giác EDB:
DC = DB (D là trung điểm của BC).
AD = ED (gt).
\(\widehat{ADC}=\widehat{EDB}\) (Đối đỉnh).
\(\Rightarrow\Delta ADC=\Delta EDB\left(c-g-c\right).\)
\(\Rightarrow\widehat{CAD}=\widehat{BED}\) (2 góc tương ứng).
\(\Rightarrow\) AC // BE.
Mà \(DK\perp BE\left(gt\right).\)
\(\Rightarrow\) \(DK\perp AC.\left(1\right)\)
Ta có: \(\widehat{AMD}=\widehat{AND}\) \(\left(\Delta MAD=\Delta NAD\right).\)
Mà \(\widehat{AMD}=90^o\left(AM\perp MD\right).\)
\(\Rightarrow\widehat{AND}=90^o.\Rightarrow AC\perp ND.\left(2\right)\)
Từ (1); (2) \(\Rightarrow N;D;K\) thẳng hàng.
KV
29 tháng 1 2019
a,
*Xét tam giác BDM và tam giác CDA, ta có:
AD = MD (đề ra)
BD = CD (đề ra)
góc BDM = góc CDA (hai góc đối đỉnh)
=> tam giác BDM = tam giác CDA (c.g.c)
=> Góc CAD = góc BMD (hai góc tương ứng)
=> AC // BM (hai góc so le trong bằng nhau)
b,
cm trên.
c,
*Xét tam giác AHD và tam giác MKD, ta có:
AD = MD (đề ra)
Góc ADH = góc MDK (hai góc đối đỉnh)
=> Tam giác AHD = tam giác MKD (cạnh huyền góc nhọn)
=> HD = KD (hai cạnh tương ứng)
Ta có:
BK = BD + DK
CH = CD + HD
Mà BD = CD
HD = KD
=> BK = CH (đpcm)
d,
*Xét tam giác AKD và tam giác MHD, ta có:
AD = MD (đề ra)
HD = KD (cm trên)
Góc HDM = góc KDA (hai góc đối đỉnh)
=> Tam giác AKD = tam giác MHD (c.g.c)
=> Góc HMD = góc KAD (hai góc tương ứng)
=> HM // AK (hai góc so le trong bằng nhau)
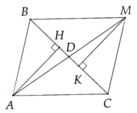
Tự vẽ hình nha