Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

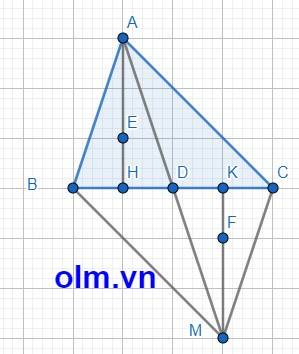
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
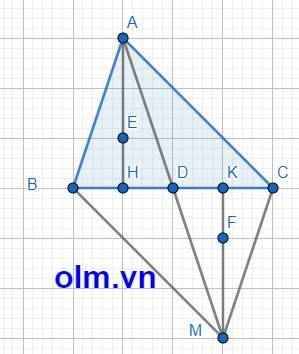
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .

a, Xét tam giác `ADC` và tam giác `MDB` có:
`DB=DC` `(g``t)`
\(\widehat{MDB}=\widehat{ADC}\) (2 góc đối đỉnh)
`DM=DA` `(g``t)`
`=>` Tam giác `ADC=` `MDB` `(c-``g-``c)`
`b,` vì tam giác `ADC=` Tam giác `MDB` (theo a)
`=> AC = BM` (2 cạnh tương ứng)
`=>` \(\widehat{ACD}=\widehat{MBD}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí sole trong
`=> AC` //`BM` (d. hiệu nhận biết) (đpcm)
c, Vì Tam giác `ADC=` Tam giác `MDB` (theo a)
`=>`\(\widehat{DAC}=\widehat{DMB}\) (2 góc tương ứng)
Xét Tam giác `ABM` và Tam giác `MCA` có:
AM chung
\(\widehat{DAC}=\widehat{DMB}\) `(CMT)`
`BM = AC (CMT)`
`=>` Tam giác `ABM =` Tam giác `MCA (c-g-c)
d, *xl cậu câu này mình bí mất r:')
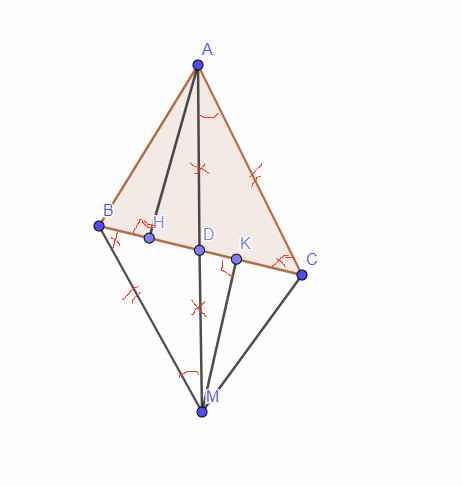

a,
*Xét tam giác BDM và tam giác CDA, ta có:
AD = MD (đề ra)
BD = CD (đề ra)
góc BDM = góc CDA (hai góc đối đỉnh)
=> tam giác BDM = tam giác CDA (c.g.c)
=> Góc CAD = góc BMD (hai góc tương ứng)
=> AC // BM (hai góc so le trong bằng nhau)
b,
cm trên.
c,
*Xét tam giác AHD và tam giác MKD, ta có:
AD = MD (đề ra)
Góc ADH = góc MDK (hai góc đối đỉnh)
=> Tam giác AHD = tam giác MKD (cạnh huyền góc nhọn)
=> HD = KD (hai cạnh tương ứng)
Ta có:
BK = BD + DK
CH = CD + HD
Mà BD = CD
HD = KD
=> BK = CH (đpcm)
d,
*Xét tam giác AKD và tam giác MHD, ta có:
AD = MD (đề ra)
HD = KD (cm trên)
Góc HDM = góc KDA (hai góc đối đỉnh)
=> Tam giác AKD = tam giác MHD (c.g.c)
=> Góc HMD = góc KAD (hai góc tương ứng)
=> HM // AK (hai góc so le trong bằng nhau)

a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD

a: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
Do đó: ΔABD=ΔECD

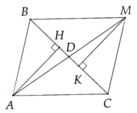
\(a,\)
Xét \(\triangle ADC\) và \(\triangle MDB\):
\(DA=DM\)
\(DC=DB\)
\(\widehat{ADC}=\widehat{MDB}\)
\(\Rightarrow\Delta ADC=\Delta MDB\left(c.g.c\right)\) \(\left(1\right)\)
\(\left(1\right)\Rightarrow AC=BM\)
\(\Rightarrow\widehat{ACD}=\widehat{MBD}\)
mà hai góc này nằm ở vị trí so le trong
\(\Rightarrow\)\(AC//BM\)
\(b,\)
\(\left(1\right)\Rightarrow\widehat{DAC}=\widehat{DMB}\)
Xét \(\triangle ABM\) và \(\triangle MCA\):
\(AM\) chung
\(BM=AC\)
\(\widehat{DAC}=\widehat{DMB}\)
\(\Rightarrow\Delta ABM=\Delta MCA\left(c.g.c\right)\).
a: Xét tứ giác ABMC có
D là trung điểm chung của AM và BC
=>ABMC là hình bình hành
=>AC//BM và AC=BM
b: Xét ΔABM và ΔMCA có
AB=MC
BM=CA
AM chung
=>ΔABM=ΔMCA