Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm BC và AD.
Tìm tổng của hai vectơ AD và NC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Ta có: \(\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)
Suy ra \(\overrightarrow {MC} = \overrightarrow {CE} \)
+) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE} \)
+) ABCD là hình bình hành nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
\(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM} \)
+) Ta có \(\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC} = \overrightarrow {AM} \)
\(\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE} \) (vì AMED là hình bình hành)
b) Ta có:
+) \(\overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM} \)
+) \(\overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
+) \(\overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
c) Ta có:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} \)
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Từ đó suy ra \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \) (đpcm)
CM
17 tháng 8 2019
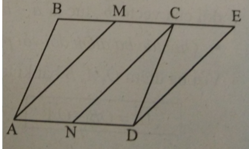
Do ABCD là hình bình hành nên: AD = BC.
Lại có; M và N lần lượt là trung điểm của BC; AD nên : AN = ND= BM = MC.
21 tháng 10 2021
a: \(\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}\)
b: \(\overrightarrow{NA}+\overrightarrow{ND}=\overrightarrow{0}\)
17 tháng 9 2020
a) N trung điểm AD \(\Rightarrow AN=\frac{AD}{2}=\frac{BC}{2}\)
M trung điểm BC \(\Rightarrow MC=\frac{BC}{2}\Rightarrow AN=MC\)mà AN//MC
nên AMCN là hình bình hành \(\Rightarrow\overrightarrow{AM}=\overrightarrow{NC}\)
b) Tương tự câu a ta được \(\hept{\begin{cases}ND=BM=\frac{1}{2}BC\\ND//BM\end{cases}}\)=> NDMB là hình bình hành=> NB//DM (1)
Xét 2 tam giác ANI và NDK: \(\hept{\begin{cases}AN=ND=\frac{AD}{2}\\\widehat{NAI}=\widehat{DNK}\left(AM//NC\right)\\\widehat{ANI}=\widehat{NDK}\left(NB//MD\right)\end{cases}\Rightarrow\Delta ANI=\Delta NDK\left(g.c.g\right)}\)
\(\Rightarrow NI=DK\)(2)
(1), (2) => \(\overrightarrow{NI}=\overrightarrow{DK}\)
MN
27 tháng 8 2021
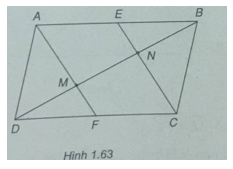
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy →DM=→MN=→NB
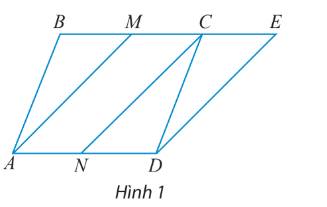
ABCD là hbh => NCMA cũng là hình bình hành
Áp dụng quy tắc hình bình hành => ↓NC + ↓MC = ↓CA ( cái này đễ cho dễ hiểu thì trước tiên gọi O là trung điểm của MN => quy tắc hình bình hành ↓NC + ↓MC = 2↓CO = ↓CA)
↓AD + ↓NC = ↓AN + ↓ND + ↓NC = ↓AC + ↓ND = ↓AC + ↓MC = 2↓CI ( với I là trung điểm của AM)
↓AM + ↓CD = ↓AB + ↓BM + ↓CD = ↓BM