Ý b thôi ạ ý a e làm đc rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)x+m-1=0\left(m-2\right)+m-1=m-1\end{matrix}\right.\)
=>A(0;m-1)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+m-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(m-2\right)=-\left(m-1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-\left(m-1\right)}{m-2}\\y=0\end{matrix}\right.\)
Vậy: \(B\left(\dfrac{-m+1}{m-2};0\right)\)
\(OA=\sqrt{\left(0-0\right)^2+\left(m-1-0\right)^2}=\sqrt{0+\left(m-1\right)^2}=\sqrt{\left(m-1\right)^2}=\left|m-1\right|\)
\(OB=\sqrt{\left(\dfrac{-m+1}{m-2}-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-\dfrac{m-1}{m-2}\right)^2+0}=\left|\dfrac{m-1}{m-2}\right|\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>\(S_{OAB}=\dfrac{1}{2}\cdot\left|m-1\right|\cdot\dfrac{\left|m-1\right|}{\left|m-2\right|}=\dfrac{1}{2}\cdot\dfrac{\left(m-1\right)^2}{\left|m-2\right|}\)
Để \(S_{OAB}=1\) thì \(\dfrac{1}{2}\cdot\dfrac{\left(m-1\right)^2}{\left|m-2\right|}=1\)
=>\(\left(m-1\right)^2=2\left|m-2\right|\)(1)
TH1: m>=2
Phương trình (1) sẽ trở thành: \(\left(m-1\right)^2=2\left(m-2\right)\)
=>\(m^2-2m+1-2m+4=0\)
=>\(m^2-4m+5=0\)
=>\(\left(m-2\right)^2+1=0\)(vô lý)
TH2: m<2
Phương trình (1) sẽ trở thành:
\(\left(m-1\right)^2=2\left(-m+2\right)\)
=>\(m^2-2m+1=-2m+4\)
=>m2=3
=>\(\left[{}\begin{matrix}m=\sqrt{3}\left(nhận\right)\\m=-\sqrt{3}\left(nhận\right)\end{matrix}\right.\)

a. \(f\left(x\right)_{max}=f\left(-2\right)=111\) ; \(f\left(x\right)_{min}=f\left(1\right)=-6\)
b. \(f\left(x\right)_{max}=f\left(-3\right)=7\) ; \(f\left(x\right)_{min}=f\left(0\right)=1\)
c. \(f\left(x\right)_{max}=f\left(4\right)=\dfrac{2}{3}\) ; \(f\left(x\right)_{min}\) ko tồn tại
d.
Miền xác định: \(D=\left[-2\sqrt{2};2\sqrt{2}\right]\)
\(y'=\dfrac{2\left(4-x^2\right)}{\sqrt{8-x^2}}=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
\(f\left(-2\sqrt{2}\right)=f\left(2\sqrt{2}\right)=0\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=4\)
\(f\left(x\right)_{max}=f\left(2\right)=4\) ; \(f\left(x\right)_{min}=f\left(-2\right)=-4\)

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)



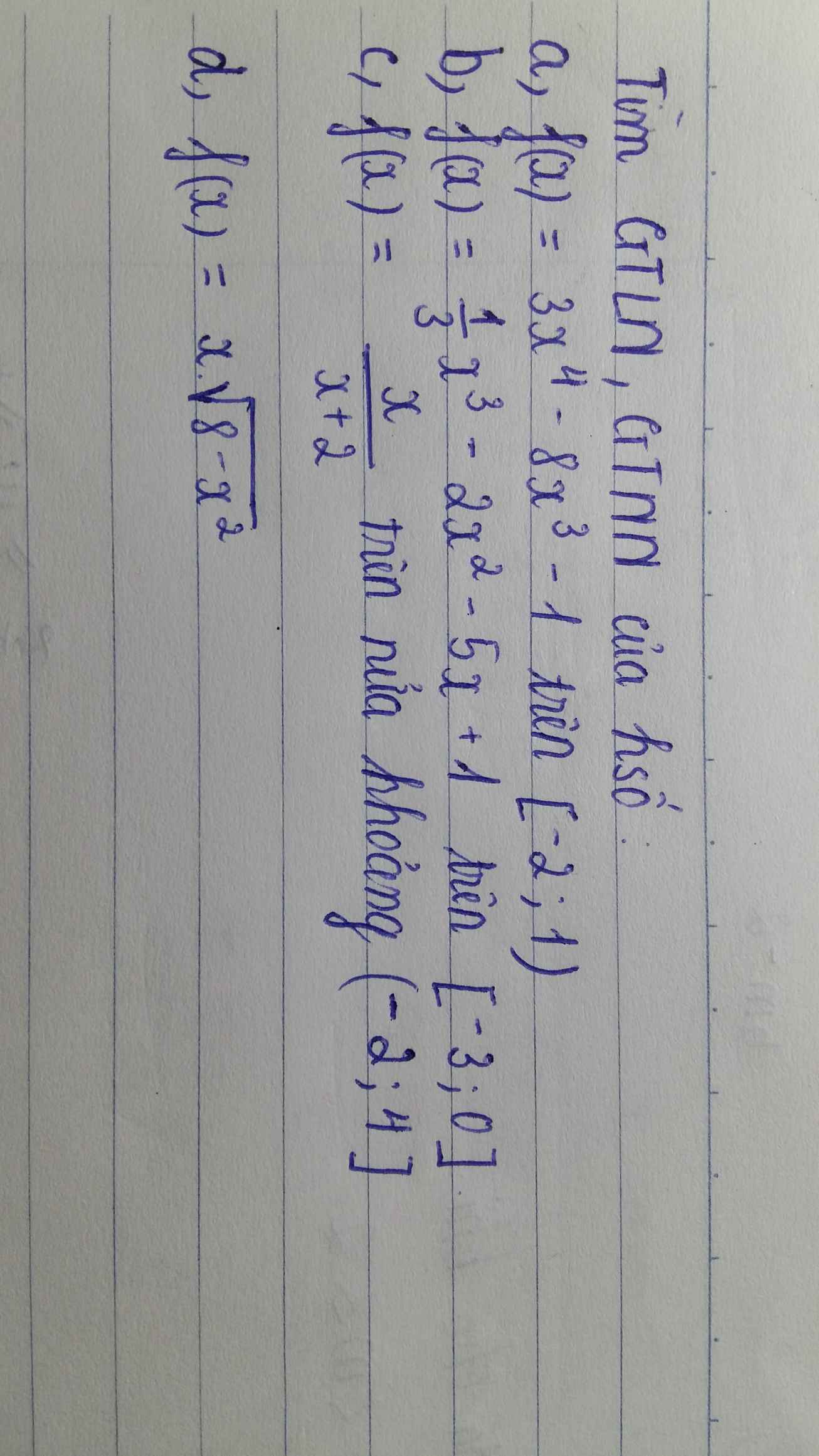


 mng ơi , đừng copy bài của các bạn khác ạ , sáng h e chỉ nhận đc 1 ý kiến giống nhau của các bạn giúp em thôi ạk
mng ơi , đừng copy bài của các bạn khác ạ , sáng h e chỉ nhận đc 1 ý kiến giống nhau của các bạn giúp em thôi ạk


