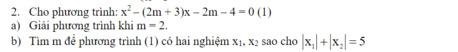T
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
\(\Delta=\left(2m+3\right)^2+4\left(2m+4\right)=4m^2+20m+25=\left(2m+5\right)^2\ge0;\forall m\)
Pt đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-3\\x_1x_2=-2m-4\end{matrix}\right.\)
\(\left|x_1\right|+\left|x_2\right|=5\Leftrightarrow x_1^2+x_2^2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(2m-3\right)^2+2\left(2m+4\right)+2\left|2m+4\right|=25\)
\(\Leftrightarrow4m^2-8m-8+4\left|m+2\right|=0\)
TH1: \(m\ge-2\)
\(\Rightarrow4m^2-8m-8+4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\) (thỏa mãn)
TH2: \(m\le-2\)
\(\Rightarrow4m^2-8m-8-4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-12m-16=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=4\left(loại\right)\end{matrix}\right.\)
Y
28 tháng 9 2023
\(a,x=36\Leftrightarrow A=\dfrac{2+\sqrt{36}}{\sqrt{36}}=\dfrac{2+6}{6}=\dfrac{4}{3}\)
\(b,B=\dfrac{x}{x-4}-\dfrac{1}{2-\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\left(dkxd:x>0,x\ne4\right)\\ =\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\\ =\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}\\ =\dfrac{x+2\sqrt{x}}{x-4}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(c,P=\dfrac{A}{B}=\dfrac{2+\sqrt{x}}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{x-4}{x}\)
Để \(Px\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\) thì \(\dfrac{x-4}{x}.x\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow x-4-\dfrac{3}{2}\sqrt{x}+\dfrac{3}{2}\le0\\ \Leftrightarrow x-\dfrac{3}{2}\sqrt{x}-\dfrac{5}{2}\le0\)
\(\Leftrightarrow x\le\dfrac{25}{4}\)
Kết hợp với điều kiện \(x>0,x\ne4,x\in Z\), ta kết luận \(S=\left\{1;2;3;5;6\right\}\)
QH
2
18 tháng 9 2021
a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
18 tháng 9 2021
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1
d.
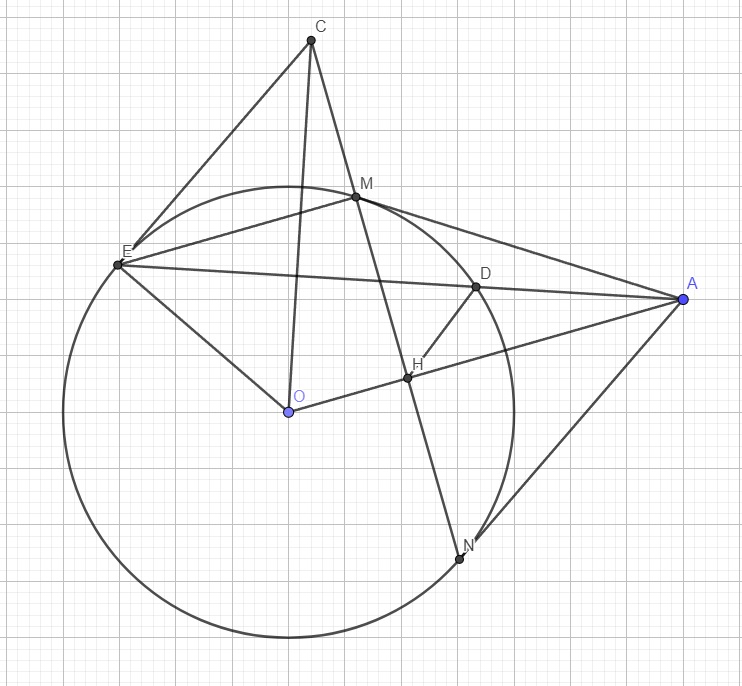
Từ câu b ta có: \(\dfrac{AD}{AO}=\dfrac{AH}{AE}\)
Xét 2 tam giác ADH và AOE có: \(\left\{{}\begin{matrix}\widehat{HAD}\text{ chung}\\\dfrac{AD}{AO}=\dfrac{AH}{AE}\end{matrix}\right.\)
\(\Rightarrow\Delta ADH\sim\Delta AOE\left(c.g.c\right)\Rightarrow\widehat{AHD}=\widehat{AEO}\)
Mà \(\widehat{AHD}+\widehat{DHO}=180^0\Rightarrow\widehat{AEO}+\widehat{DHO}=180^0\)
\(\Rightarrow\) Tứ giác DHOE nội tiếp
Lại có E và H cùng nhìn OC dưới 1 góc vuông \(\Rightarrow CHOE\) nội tiếp đường tròn đường kính OC
\(\Rightarrow C,D,H,O,E\) cùng thuộc đường tròn đường kính OC
\(\Rightarrow\widehat{CDO}\) là góc nt chắn nửa đường tròn (do OC là đường kính)
\(\Rightarrow CD\perp OD\)
\(\Rightarrow CD\) là tiếp tuyến của (O) tại D
\(\Rightarrow C\) là giao điểm 2 tiếp tuyến của (O) tại D và E
\(\Rightarrow CE=CD\) (t/c 2 tiếp tuyến cắt nhau)
Mà \(OD=OE=R\)
\(\Rightarrow OC\) là trung trực của DE \(\Rightarrow OC\perp DE\)
Theo gt I là trung điểm DE \(\Rightarrow OI\perp DE\)
\(\Rightarrow\)Đường thẳng OC trùng đường thẳng OC\(\Rightarrow O,I,C\) thẳng hàng
8 tháng 12 2023
Câu 1:
1:
a: \(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=3\cdot2=6\)
b: \(3x^2-12x=0\)
=>\(3x\cdot x-3x\cdot4=0\)
=>\(3x\left(x-4\right)=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2:
a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+\dfrac{3}{2}\)
=>\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\dfrac{1}{2}\cdot\left(-3\right)^2=\dfrac{1}{2}\cdot9=4,5\)
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
b: Gọi (d1): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Thay x=2 và y=2 vào (d), ta được:
\(a\cdot2+b=2\)
=>2a+b=2
=>b=2-2a
=>y=ax+2-2a
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=ax+2-2a\)
=>\(\dfrac{1}{2}x^2-ax-2+2a=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot\dfrac{1}{2}\cdot\left(2a-2\right)\)
\(=a^2-2\left(2a-2\right)=a^2-4a+4=\left(a-2\right)^2\)
Để (P) tiếp xúc với (d1) thì Δ=0
=>a-2=0
=>a=2
=>b=2-2a=2-4=-2
Vậy: Phương trình đường thẳng cần tìm là y=2x-2
QN
0