Cho hình thang ABCD(AB // CD, AB < CD).
Chứng minh rằng: CD-AB < AD+BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
0
KT
0
8 tháng 8 2017
2, Tự vẽ hình nha bạn :
Trên nửa mặt phẳng bờ \(CD\) có chứa điểm \(A\) , vẽ tia \(Cx\) sao cho \(\widehat{DCx}=\widehat{ADC}\) , \(Cx\) cắt \(AB\) tại \(E\)
Ta có : \(\widehat{DCB}< \widehat{ADC}\left(gt\right)\)
\(\Rightarrow\widehat{DCB}=\widehat{DCx}\)
\(\Rightarrow\) Tia \(CB\) nằm giữa hai tia \(CD\) và \(CE\)
\(\Rightarrow\) Điểm \(B\) nằm giữa 2 điểm \(A\) và \(E\)
Tứ giác : \(AECD\) có : \(AE//CD\) và \(\widehat{ADC}=\widehat{DCE}\)
\(\Rightarrow\)\(AECD\) là hình thang cân
\(\Rightarrow\Delta ADE=\Delta ECA\left(c-g-c\right)\) ( TỰ CHỨNG MINH NHÉ )
\(\Rightarrow\widehat{AED}=\widehat{CAE}\)
Gọi \(O\) là giao điểm của\(AC\) và \(BD\)
\(\Delta OAB\) có \(\widehat{DBE}\) là góc ngoài
\(\Rightarrow\widehat{DBE}>\widehat{OAB}\)
\(\Rightarrow\widehat{DBE}>\widehat{BED}\)
\(\Delta BOE\) có : \(\widehat{DBE}>\widehat{BEC}\)
\(\Rightarrow DE>BD\)
Mà \(DE=AC\)
\(\Rightarrow AC>BD\left(dpcm\right)\)
LN
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
18 tháng 9 2018
Hạ AH và BK vuông góc với CD (H; k thuộc CD)
Dễ dàng c/m được ABKH là hình vuông => AB=KH
=> CD-AB=CD-KH=(DH+CK)
Xét tg vuông ADH có DH<AD
Xét tg vuông BCK có CK<BC
Mà AD=BC (hình thang ABCD là hình thang cân)
=> CK<AD
=> DH+CK<2AD
=> CD-AB<2AD
CM
1 tháng 11 2017
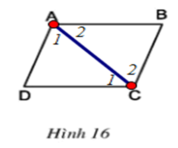
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
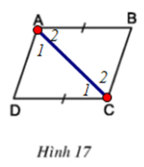
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Từ D dóng DE⊥ABDE⊥AB, từ C dóng CE⊥EFCE⊥EF
Ta có : DC = EF (DCEF hình chữ nhật)(tự CM nhé, dễ lắm)
⇒DC−AB=EF−AB=AF+BE⇒DC−AB=EF−AB=AF+BE(1)
Xét ΔAFD(ˆF=90o)ΔAFD(F^=90o) có :
AD>AFAD>AF (n/x)
Xét ΔBEC(ˆE=90o)ΔBEC(E^=90o) có :
BC>BEBC>BE (n/x)
⇒AF+BE<AD+BC⇒AF+BE<AD+BC(2)
Từ (1) và (2)
⇒DC−AB<AD+BC
Từ D dóng DE vuông AB, từ C dóng CE vuông EF.
Ta có : DC = EF (DCEF hình chữ nhật)
Ta có : DC - AB = EF - AB = AF + BE (*)
Xét ▲AFD (90 độ) có :
AD > AF (n/x)
Xét ▲BEC (có E = 90 độ)
=> AF + BE < AD + BC (**)
Từ (*) (**)
=> DC - AB < AD + BC