Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAMB vuông tại M và ΔANC vuông tạiN có
góc A chung
=>ΔAMB đồng dạng vơi ΔANC
=>AM/AN=AB/AC
=>AM*AC=AB*AN; AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
=>góc AMN=góc ABC
\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.
TAM GIÁC ĐỒNG DẠNG
1, a) Tỉ số hai đoạn thẳng AB và AC : \(\frac{AB}{AC}=\frac{6}{15}\)
b) Tỉ số hai đoạn thẳng AB và AC . : \(\frac{AB}{AC}=\frac{6}{18}=\frac{1}{3}\)
2, ΔMNP ~ ΔABC thì : \(\frac{MN}{AB}=\frac{NP}{BC}=\frac{MP}{AC}\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
Bạn ơi D ở đâu vậy ?
b) Cho ΔABCΔABC có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
Xét \(\Delta ABC\) có AD là phân giác
\(\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\Rightarrow BD=\frac{AB.CD}{AC}=3cm\)
5. a) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k = 2. Tìm tỉ số SDÈFvà SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=2^2=4\)
b) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số SDEF và SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
6. Cho ΔABC..Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho AD/AB=AE/AC Kết luận nào sai ❓
A. ΔADE∼ΔABC B. DE//BC
C. AE/AD=AC/AB D. ΔADE=ΔABC
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.ΔABC∼ΔDEF B. ΔABC∼ΔEDF
C. ΔABC∼ΔDFE D.ΔABC∼ΔFED
\(Pytago:\)
\(AC^2=BC^2-AB^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)
Áp dung HTL trong tam giác vuông ABC có :
\(AB\cdot AC=AH\cdot BC\\ \Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{3\cdot4}{5}=2.4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-4^2=9\)
hay \(AC=\sqrt{9}=3cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB\cdot AC=BC\cdot AH\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Vậy: AH=2,4cm
`a)` Xét `\triangle ABC` vuông tại `A` có: `\hat{B}+\hat{C}=90^o`
Xét `\triangle ABH` vuông tại `H` có: `\hat{B}+\hat{A_1}=90^o`
`=>\hat{C}=\hat{A_1}`
Xét `\triangle ABC` và `\triangle HBA` có:
`{:(\hat{C}=\hat{A_1}),(\hat{B}\text{ là góc chung}):}}=>\triangle ABC` $\backsim$ `\triangle HBA` (g-g)
`b)` Ta có: `BC=HB+HC=4+9=13(cm)`
Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao
`@AH=\sqrt{BH.HC}=6 (cm)`
`@AB=\sqrt{BH.BC}=2\sqrt{13}(cm)`
Ta có: `\hat{DEA}=\hat{ADH}=\hat{AEH}=90^o`
`=>` Tứ giác `AEHD` là hcn `=>DE=AH=6(cm)`
`c)` Xét `\triangle AHB` vuông tại `H` có: `HD \bot AB=>AH^2=AD.AB`
Xét `\triangle AHC` vuông tại `H` có: `HE \bot AC=>AH^2=AE.AC`
`=>AD.AB=AE.AC`
a. Ta có: 32+42=52
9+16=25
=> Tam giác ABC là tam giác vuông tại A (định lí Py-ta-go đảo)
b. Xét tam giác ABD và tam giác DBE có:
góc A= góc E (=90º)
góc ABD=góc DBE (BD là tia phân giác của góc B)
BD là cạnh huyền chung
=> tam giác ABD = tam giác DBE(cạnh huyền- góc nhọn)
=> DA=DE (2 cạnh tương ứng)
c. Xét tam giác ADF và tam giác EDC có:
góc A= góc E (=90º)
góc ADF=góc EDC (đối đỉnh)
AD=DC (c/m ở câu b)
=> tam giác ADF = tam giác EDC (cạnh góc vuông-góc nhọn kề)
Ta có: góc A>góc C (vì A là góc vuông, C là góc nhọn)
=> DF > DE (quan hệ giữa đường xiên và hình chiếu)
a) Xét 2 tam giác ABC
Áp dụng định lý Pytago đảo có:
BC2 = 5252 = 15
AB2+AC2=32+42=9+16=25
=> Tam giác ABC vuông tại A
b)
Xét 2 tam giác vuông ABD và tam giác EBD có:
Góc B1 = góc B2 (gt)
BD là cạnh huyền chung
=> Tam giác ABD = tam giác EBD (cạnh huyền- góc nhọn)
=> AD=ED (đpcm)
c)
Xét 2 tam giác vuông ADF và tam giác EDC có:
Góc D1 = góc D2 (đối đỉnh)
AD = ED (vì tam giác ABD = tam giác EBD)
=> tam giác ADF = tam giác EDC (cạnh góc vuông- góc nhọn kề cạnh ấy)
=> DF = DC (2 cạnh tương ứng)
Xét tam giác EDC vuông tại E có:
DC > DE ( cạnh huyền > cạnh góc vuông)
mà DF = DC
=> DF > DE (đpcm)
CHÚC BN HỌC TỐT ^-^
a/ ΔABC có: \(AB^2+AC^2=BC^2\) (vì 32 + 42 = 52)
=> ΔABC vuông tại A
b) Ta có: \(\widehat{BAC}+\widehat{BAD}=180^0\) (kề bù)
=> \(\widehat{BAD}=180^0-\widehat{BAC}=180^0-90^0=90^0\)
Xét ΔABC và ΔABD ta có:
AD = AC (GT)
\(\widehat{BAC}=\widehat{BAD}\left(=90^0\right)\)
AB: cạnh chung
=> ΔABC = ΔABD (c - g - c)
=> BC = BD (2 cạnh tương ứng)
=> ΔBCD cân tại B
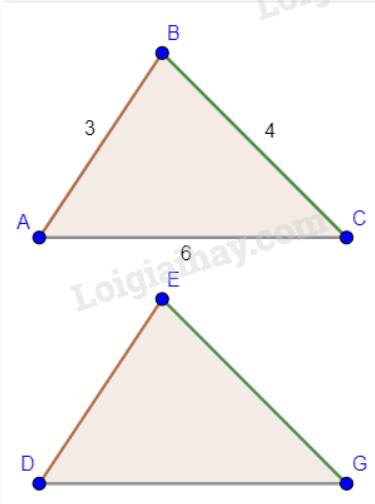
a)
\(AB^2+AC^2=3^2+4^2=9+16=25\left(cm\right)\)
\(BC^2=5^2=25\left(cm\right)\)
=> tam giác ABC vuông tại A
b)
xét 2 tam giác vuôgn ABD và EBD có:
BD(chung)
ABD=EBD(gt)
=> tam giác ABD=EBD(CH-GN)
=> DA=DE
c)
xét tam giác ADF và tam giác EDC có:
AD=DE(theo câu a)
FAD=DEC=90
ADF=EDC(2 góc đối đỉnh)
=> tam giác ADF=EDC(g.c.g)
=> DC=FF
ta có tam giác ADF có A=90=> FD là cạnh lớn nhất trong tam giác ADF
=> FD>AD mà AD=DE( theo câu b)=> DF>DE