ML
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ML
1
M
9 tháng 4 2022
a)Xét ΔAKB và ΔCAB có:
\(\widehat{AKB}=\widehat{BAC}=90^o\left(gt\right)\)
\(\widehat{C}chung\)
⇒ΔAKB ~ ΔCAB(g-g)
b)Xét ΔABC có:OB=OC(O là trung điểm BC);BI=AI(I là trung điểm AB)
⇒OI là đường TB ΔABC(đ/n)
⇒OI//AC(t/c)
Mà AC⊥AB(gt) ⇒OI⊥AB(t/c)
Xét ΔBOI và ΔBAK có:
\(\widehat{BIO}=\widehat{BKA}=90^o\)
\(\widehat{B}\) chung
⇒ΔBOI ~ ΔBAK(g-g)
⇒\(\dfrac{BI}{BK}=\dfrac{BO}{BA}\Rightarrow BI.BA=BK.BO\)(đpcm)
21 tháng 12 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
16 tháng 4 2022
a: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
hay AM⊥BC
Xét ΔAEC vuông tại E và ΔADB vuông tại D có
góc EAC chung
Do đó: ΔAEC\(\sim\)ΔADB
b: Xét ΔAED và ΔACB có
AE/AC=AD/AB
góc EAD chung
Do đó: ΔAED\(\sim\)ΔACB
29 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
AM=BC/2=5cm
b:
ΔAEH vuông tại A có AI là trung tuyến
nên IH=IA
=>góc IHA=góc IAH
góc IAH+góc MAB
=góc MBA+góc IHA=90 độ
=>góc IAM=90 độ
=>AI vuông góc AM
14 tháng 1
Trong 1 ngày thì máy thứ nhất cày được: \(\dfrac{1}{20}\)(cánh đồng)
Trong 1 ngày thì máy thứ hai cày được \(\dfrac{1}{30}\)(cánh đồng)
Trong 1 ngày thì hai máy cày được \(\dfrac{1}{20}+\dfrac{1}{30}=\dfrac{3}{60}+\dfrac{2}{60}=\dfrac{5}{60}=\dfrac{1}{12}\)(cánh đồng)
=>Hai máy cần \(1:\dfrac{1}{12}=12\left(ngày\right)\) để cày xong cánh đồng
MN
22 tháng 5 2021
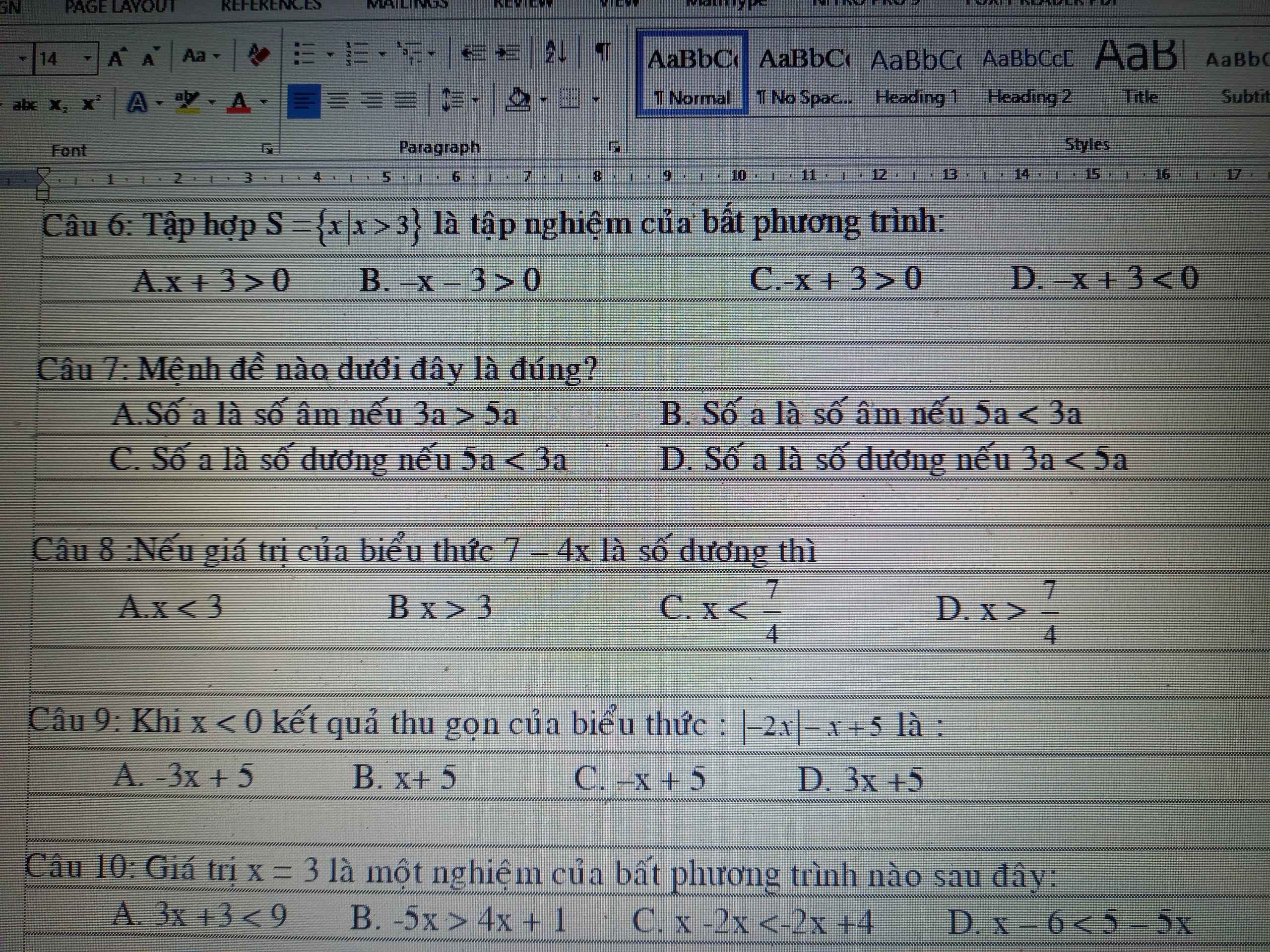
Từ hình vẽ ta thấy :
\(x< -1\)
\(\Leftrightarrow x+4< 4+\left(-1\right)\)
\(\Leftrightarrow x+4< 3\)
\(\Rightarrow C\)
T
21 tháng 11 2023
1. ĐKXĐ: \(x\ne5\)
\(\dfrac{3x+1}{x-5}+\dfrac{-2x-6}{x-5}\)
\(=\dfrac{3x+1-2x-6}{x-5}\)
\(=\dfrac{x-5}{x-5}\)
\(=1\)
2. ĐKXĐ: \(x\ne\pm1\)
\(\dfrac{x+1}{2x-2}-\dfrac{x^2+3}{2x^2-2}\)
\(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{x^2+3}{2\left(x^2-1\right)}\)
\(=\dfrac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}-\dfrac{x^2+3}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+2x+1-x^2-3}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2x-2}{\left(2x-2\right)\left(x+1\right)}\)
\(=\dfrac{1}{x+1}\)
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
r) \(100x^2-\left(x^2-25\right)^2\)
\(=\left(10x\right)^2-\left(x^2+25\right)^2\)
\(=\left(10x-x^2-25\right)\left(10x+x^2+25\right)\)
\(=\left(-x^2+10x-25\right)\left(x^2+10x+25\right)\)
\(=-\left(x-5\right)^2\left(x+5\right)^2\)
v) \(\left(x+y\right)^2-2\left(x+y\right)+1\)
\(=\left(x+y\right)^2-2\left(x+y\right)\cdot1+1^2\)
\(=\left(x+y-1\right)^2\)
y) \(12y-36-y^2\)
\(=-y^2+12x-36\)
\(=-\left(y^2-12x+36\right)\)
\(=-\left(y-6\right)^2\)
12 tháng 8 2023
r: =(10x)^2-(x^2+25)^2
=(10x-x^2-25)(10x+x^2+25)
=-(x^2-10x+25)(x+5)^2
=-(x-5)^2(x+5)^2
t: =(2x-1)^2-(x+1)^2
=(2x-1-x-1)(2x-1+x+1)
=3x*(x-2)
v: =(x+y)^2-2(x+y)*1+1^2
=(x+y-1)^2
u: =(x-y+5)^2-2(x-y+5)*1+1^2
=(x-y+5-1)^2
=(x-y+4)^2
x: =-(x^2+2xy+y^2)
=-(x+y)^2
y: =-(y^2-12y+36)
=-(y-6)^2
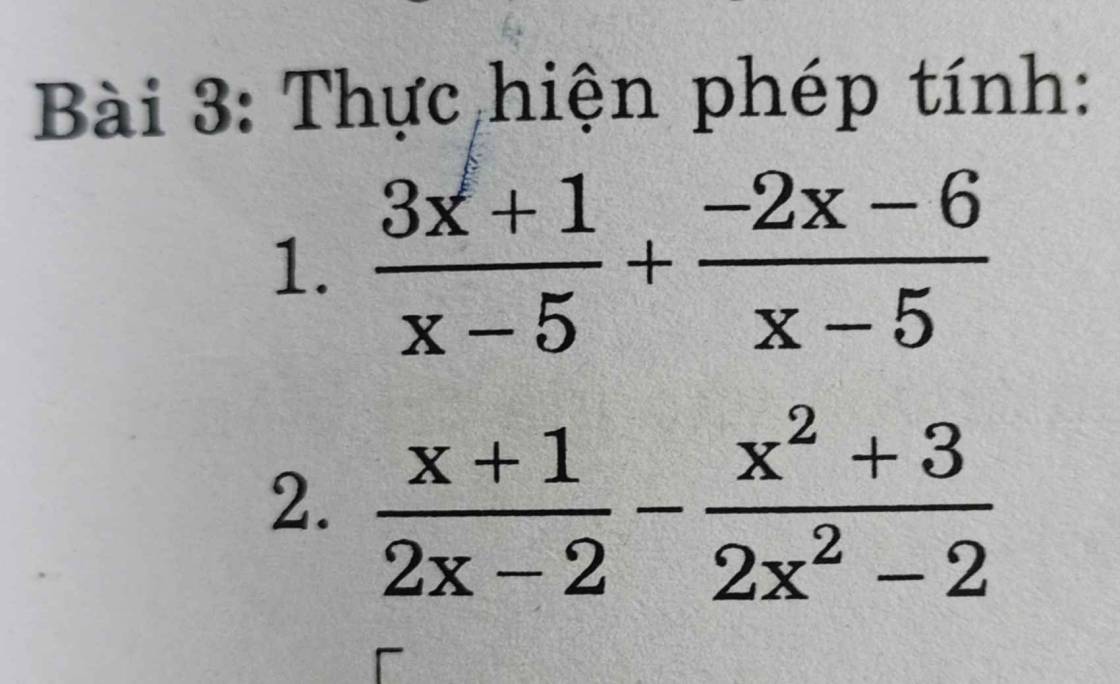
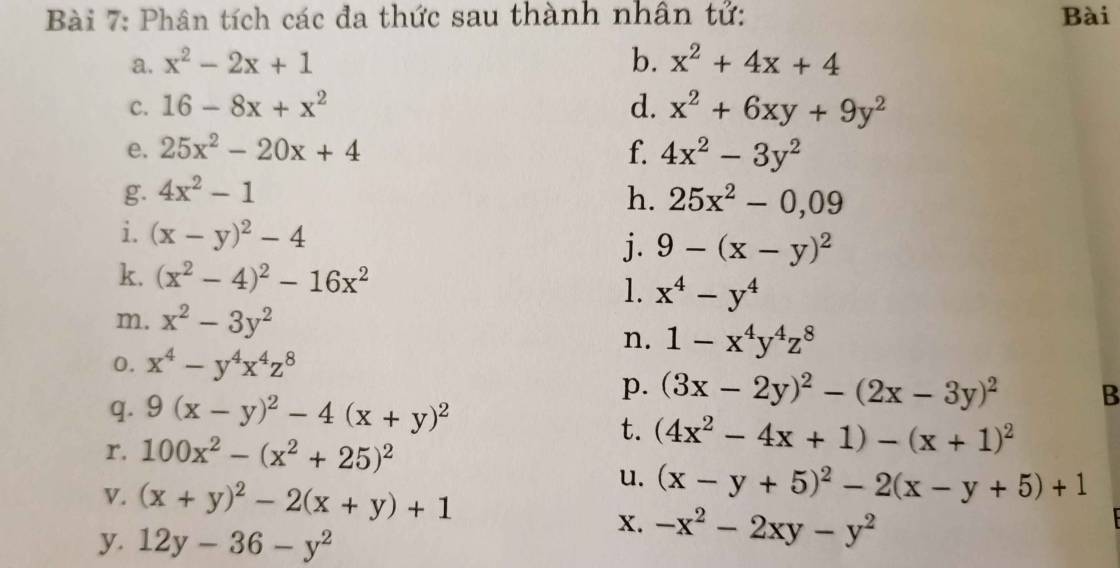
Xin lỗi em mới lớp ... 4 thôi hà :(