K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
AM=BC/2=5cm
b:
ΔAEH vuông tại A có AI là trung tuyến
nên IH=IA
=>góc IHA=góc IAH
góc IAH+góc MAB
=góc MBA+góc IHA=90 độ
=>góc IAM=90 độ
=>AI vuông góc AM
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
r) \(100x^2-\left(x^2-25\right)^2\)
\(=\left(10x\right)^2-\left(x^2+25\right)^2\)
\(=\left(10x-x^2-25\right)\left(10x+x^2+25\right)\)
\(=\left(-x^2+10x-25\right)\left(x^2+10x+25\right)\)
\(=-\left(x-5\right)^2\left(x+5\right)^2\)
v) \(\left(x+y\right)^2-2\left(x+y\right)+1\)
\(=\left(x+y\right)^2-2\left(x+y\right)\cdot1+1^2\)
\(=\left(x+y-1\right)^2\)
y) \(12y-36-y^2\)
\(=-y^2+12x-36\)
\(=-\left(y^2-12x+36\right)\)
\(=-\left(y-6\right)^2\)
12 tháng 8 2023
r: =(10x)^2-(x^2+25)^2
=(10x-x^2-25)(10x+x^2+25)
=-(x^2-10x+25)(x+5)^2
=-(x-5)^2(x+5)^2
t: =(2x-1)^2-(x+1)^2
=(2x-1-x-1)(2x-1+x+1)
=3x*(x-2)
v: =(x+y)^2-2(x+y)*1+1^2
=(x+y-1)^2
u: =(x-y+5)^2-2(x-y+5)*1+1^2
=(x-y+5-1)^2
=(x-y+4)^2
x: =-(x^2+2xy+y^2)
=-(x+y)^2
y: =-(y^2-12y+36)
=-(y-6)^2
17 tháng 9 2021
Bài 4
Ta có: \(\left(4+2x\right)\left(4-2x\right)+\left(2x-3\right)^2=2\)
\(\Leftrightarrow16-4x^2+4x^2-12x+9=2\)
\(\Leftrightarrow-12x=-23\)
hay \(x=\dfrac{23}{12}\)
MN
22 tháng 5 2021
Từ hình vẽ ta thấy :
\(x< -1\)
\(\Leftrightarrow x+4< 4+\left(-1\right)\)
\(\Leftrightarrow x+4< 3\)
\(\Rightarrow C\)
KN
5 tháng 3 2020
\(\Leftrightarrow6x^2+10x-6x-10=0\)
\(\Leftrightarrow6x^2+4x-10=0\)
Ta có \(\Delta=4^2+4.6.10=256,\sqrt{\Delta}=16\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-4+16}{12}=1\\x=\frac{-4-16}{12}=\frac{-5}{3}\end{cases}}\)
5 tháng 3 2020
e mới lớp 5 nên chưa chắc ạ >:
\(2x\left(3x+5\right)-6x-10=0\)
\(=>6x^2+10x-6x-10=0\)
\(=>6x.\left(x-1\right)+10.\left(x-1\right)=0\)
\(=>\left(6x+10\right)\left(x-1\right)=0\)
\(=>\orbr{\begin{cases}6x+10=0\\x-1=0\end{cases}=>\orbr{\begin{cases}x=\frac{-10}{6}\\x=1\end{cases}}}\)
19 tháng 6 2023
a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
ML
2
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
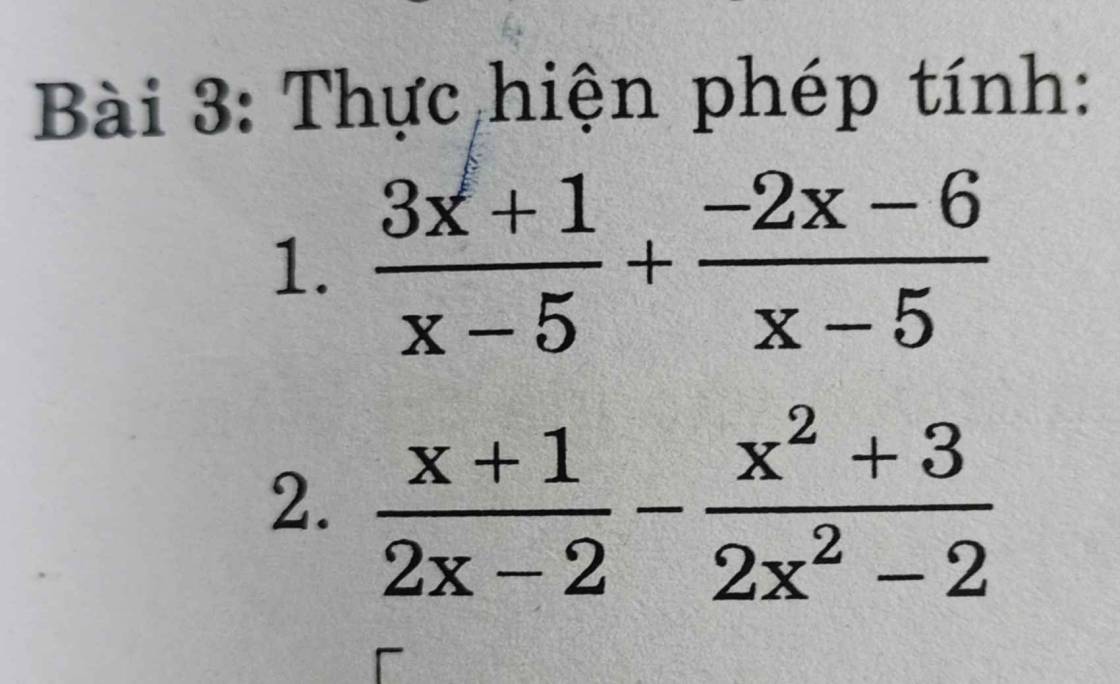
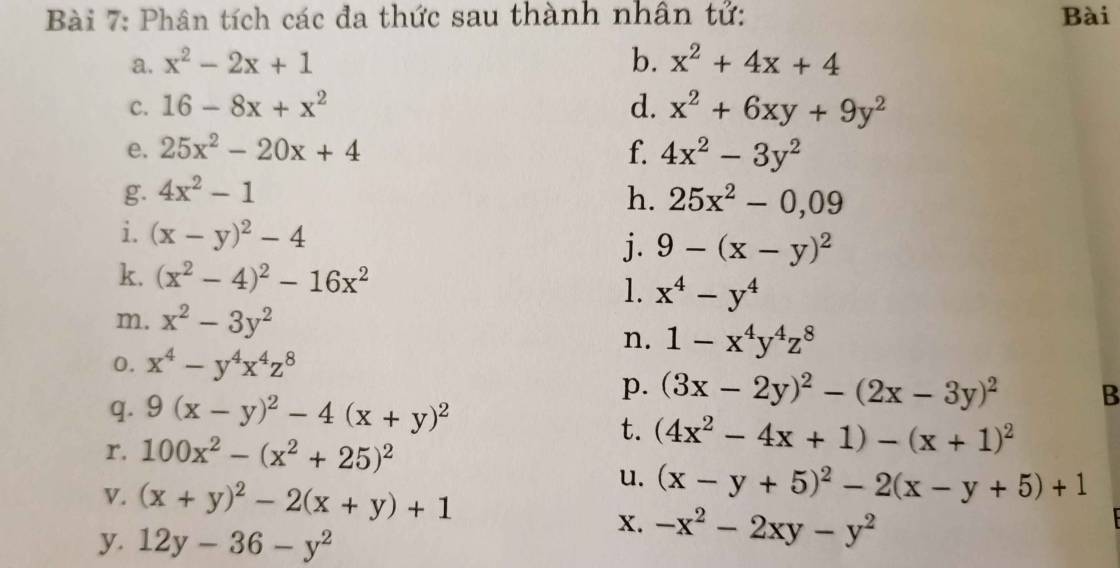
1. ĐKXĐ: \(x\ne5\)
\(\dfrac{3x+1}{x-5}+\dfrac{-2x-6}{x-5}\)
\(=\dfrac{3x+1-2x-6}{x-5}\)
\(=\dfrac{x-5}{x-5}\)
\(=1\)
2. ĐKXĐ: \(x\ne\pm1\)
\(\dfrac{x+1}{2x-2}-\dfrac{x^2+3}{2x^2-2}\)
\(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{x^2+3}{2\left(x^2-1\right)}\)
\(=\dfrac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}-\dfrac{x^2+3}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+2x+1-x^2-3}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2x-2}{\left(2x-2\right)\left(x+1\right)}\)
\(=\dfrac{1}{x+1}\)
Em cảm ơn nhìu ạ 😍❤️