Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
TH1: Nhóm có đúng 3 học sinh có 
cách chọn
TH2: Nhóm có đúng 4 học sinh có 
cách chọn
TH3: Nhóm có đúng 5 học sinh có 
cách chọn
TH4: Nhóm có đúng 6 học sinh có 
cách chọn
TH5: Nhóm có đúng 7 học sinh có 
cách chọn
TH6: Nhóm có đúng 8 học sinh có 
cách chọn
TH7: Nhóm có đúng 9 học sinh có 
cách chọn
Vậy tổng số có 24 + 72 + 98 + 76 + 35 + 9 + 1 = 315 cách.
Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)
Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có 
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có 
cách.
Do đó trường hợp này có 
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có 
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có 
cách.
Do đó trường hợp này có 
cách.
Suy ra số phần tử của biến cố là 
Vậy xác suất cần tính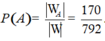 
Chọn C.
Chọn A.
Lời giải.
Không gian mẫu là số cách chọn 2 phần thưởng trong số 12 phần thưởng
Suy ra số phần tử của không gian mẫu là Ω = C 12 2 = 66
Gọi A là biến cố ""Bạn An và bạn Bình có phần thưởng giống nhau"".
Để tìm số phần tử của A, ta làm như sau
Gọi x là cặp số gồm 2 quyển Toán và Vật Lí
y là số cặp gồm 2 quyển Toán và Hóa Học;
z là số cặp gồm 2 quyển Vật Lí và Hóa Học
Ta có hệ phương trình
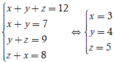
Suy ra số phần tử của biến cố A là
Ω A = C 3 2 + C 4 2 + C 5 2
Vậy xác suất cần tính P ( A ) = 19 66
Đáp án C.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 3 học sinh trong 10 học sinh có C 10 3 cách => n ( Ω ) = C 10 3 = 120 .
Gọi X là biến cố trong 3 học sinh được chọn có ít nhất một học sinh nữ
Ta xét các trường hợp sau:
TH1. Chọn 1 học sinh nữ và 2 học sinh nam => có C 7 2 . C 3 1 = 63 cách.
TH2. Chọn 2 học sinh nữ và 1 học sinh nam => có C 7 1 . C 3 2 = 21 cách.
TH3. Chọn 3 học sinh nữ và 0 học sinh nam => có C 3 3 = 1 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 63 + 21 + 1 = 85.
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 85 120 = 17 24 .
Nếu chọn đề tài về lịch sử có 8 cách.
Nếu chọn đề tài về thiên nhiên có 7 cách.
Nếu chọn đề tài về con người có 10 cách.
Nếu chọn đề tài về văn hóa có 6 cách.
Theo qui tắc cộng, ta có 8+ 7+ 10 + 6 = 31 cách chọn.
Chọn đáp án C.
Khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng là
\(M\left( 6 \right) = 75 - 20\ln \left( {6 + 1} \right) = 36,08179702\)%.