Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp.
Chia ra các khả năng có thể có của học sinh các lớp. Tính số cách chọn có thể có của mỗi trường hợp này. Lấy tổng kết quả các khả năng ở trên lại.
Lời giải chi tiết.
Ta xét các trường hợp sau.
Có 1 học sinh lớp 12C có 2 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có 2 C 3 2 C 4 2 = 36
cách chọn.
Có 1 học sinh lớp 12C có 3 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có 2 C 3 3 C 4 1 = 8 cách chọn.
Có 1 học sinh lớp 12C có 1 học sinh lớp 12B và 3 học sinh lớp 12A khi đó ta có 2 C 3 1 C 4 3 = 24 cách chọn.
Có 2 học sinh lớp 12C có 1 học sinh lớp 12B và 2 học sinh lớp 12A khi đó ta có C 3 1 C 4 2 = 18 cách chọn.
Có 2 học sinh lớp 12C có 2 học sinh lớp 12B và 1 học sinh lớp 12A khi đó ta có C 3 2 C 4 1 = 12 cách chọn.
Vậy tổng số cách chọn là 36 + 8 + 24 + 18 + 12 = 98
Đáp án A
Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp
TH1.1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C
⇒ có C 4 1 . C 3 2 . C 2 2 = 12 cách
TH2.2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C
⇒ có C 4 3 . C 3 1 . C 2 2 = 18 cách
TH3.3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 3 . C 3 1 . C 2 1 = 24 cách
TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 1 . C 3 3 . C 2 1 = 8 cách
TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C
⇒ có C 4 2 . C 3 2 . C 2 1 = 36 cách
[Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = [Số cách chọn 4 em trong 12 em] - [số cách chọn mà mỗi lớp có ít nhất 1 em]
Mà:
[Số cách chọn 4 em trong 12 em] = \(C^4_{12}=\frac{12!}{4!\left(12-4\right)!}=495\)
[số cách chọn mà mỗi lớp có ít nhất 1 em] = [Số cách chọn lớp A có 2 hs, lớp B, C mỗi lớp có 1 hs] + [Số cách chọn lớp B có 2 hs, lớp A, C mỗi lớp có 1 hs] + [Số cách chọn lớp C có 2 hs, lớp A, B mỗi lớp có 1 hs]
= \(C^2_5.C^1_4.C^1_3+C^1_5.C^2_4.C^1_3+C^1_5.C^1_4.C^2_3\)
= 120 + 90 + 60
= 270
Vậy [Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = 495 - 270 =....
Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì 
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho 
là:
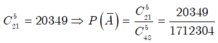
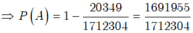
Mỗi tổ ít nhất 2 nữ \(\Rightarrow\) ta có 3 trường hợp: (2;2;3); (2;3;2); (3;2;2)
TH1: (2;2;3)
Tổ 1: chọn 2 nữ từ 7 nữ có \(C_7^2\) cách, chọn 8 nam từ 26 nam có \(C_{26}^8\) cách
Tổ 2: chọn 2 nữ từ 5 nữ còn lại: \(C_5^2\) ; chọn 9 nam từ 18 nam còn lại: \(C_{18}^9\)
Tổ 3: chọn 3 nữ từ 3 nữ còn lại: \(C_3^3\) ; chọn 9 nam từ 9 nam còn lại: \(C_9^9\)
\(\Rightarrow C_7^2.C_{26}^8+C_5^3.C_{18}^8+C_2^2.C_{10}^{10}\)
Hoàn toàn tương tự, ở TH2 ta được số cách:
\(C_7^2.C_{26}^8+C_5^3.C_{18}^9+C_2^2.C_9^9\)
TH3 ta được số cách: \(C_7^3.C_{26}^7+C_4^2.C_{19}^9+C_2^2.C_{10}^{10}\)
Cộng 3 trường hợp lại ta được kết quả cần tìm
a. Chọn bất kì 5 học sinh từ 50 học sinh có: \(C_{50}^5\) cách
b. Lớp có 20 học sinh nam. Chọn 5 bạn trong đó có 2 bạn nam (suy ra 3 bạn nữ) đồng nghĩa: chọn 2 nam từ 20 nam và 3 nữ từ 30 nữ
\(\Rightarrow\) Có \(C_{20}^2.C_{30}^3\) cách
c. Số cách chọn 5 bạn toàn là nữ: \(C_{30}^5\) cách
Số cách chọn 5 bạn có ít nhất 1 nam: \(C_{50}^5-C_{30}^5\) cách
Số cách chia lớp thành 3 tổ thỏa yêu cầu có 3 trường hợp
* TH1: Tổ 1 có 3 nữ, 7 nam có 
cách chọn
Tổ 2 có 2 nữ, 9 nam có 
cách chọn
Tổ 3 có 2 nữ, 10 nam có 
cách chọn
Vậy có 
cách chia thành 3 tổ trong TH này
* TH2: Tổ 2 có 3 nữ và hai tổ còn lại có 2 nữ, tương tự tính được 
cách chia.
* TH3: Tổ 3 có 3 nữ và hai tổ còn lại có 2 nữ, tương tự tính được 
cách chia.
Vậy có tất cả 
cách chia
Chọn D.
Số cách chia lớp thành 3 tổ thỏa yêu cầu có 3 trường hợp
* TH1: Tổ 1 có 3 nữ, 7 nam có C 7 3 C 26 7 cách chọn
Tổ 2 có 2 nữ, 9 nam có C 4 2 C 19 9 cách chọn
Tổ 3 có 2 nữ, 10 nam có C 2 2 C 10 10 cách chọn
Vậy có C 7 3 C 26 7 C 4 2 C 19 9 cách chia thành 3 tổ trong TH này
* TH2: Tổ 2 có 3 nữ và hai tổ còn lại có 2 nữ, tương tự tính được C 7 2 C 26 8 C 5 3 C 18 8 cách chia.
* TH3: Tổ 3 có 3 nữ và hai tổ còn lại có 2 nữ, tương tự tính được C 7 2 C 26 8 C 5 2 C 18 9 cách chia.
Vậy có tất cả C 7 3 C 26 7 C 4 2 C 19 9 + C 7 2 C 26 8 C 5 3 C 18 8 + C 7 2 C 26 8 C 5 2 C 18 9 cách chia.
Chọn D.
Chọn B
TH1: Nhóm có đúng 3 học sinh có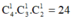
cách chọn
TH2: Nhóm có đúng 4 học sinh có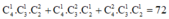
cách chọn
TH3: Nhóm có đúng 5 học sinh có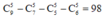
cách chọn
TH4: Nhóm có đúng 6 học sinh có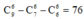
cách chọn
TH5: Nhóm có đúng 7 học sinh có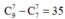
cách chọn
TH6: Nhóm có đúng 8 học sinh có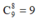
cách chọn
TH7: Nhóm có đúng 9 học sinh có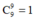
cách chọn
Vậy tổng số có 24 + 72 + 98 + 76 + 35 + 9 + 1 = 315 cách.