Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
![]()
![]()
Suy ra phương trình mặt phẳng (ABC) là x+ y + z +1=0
Diện tích tam giác ABC là
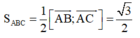
Góc giữa hai mặt phẳng (ABC) và α là
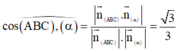
Khi đó diện tích tam giác A'B'C' là S A ' B ' C ' = S A B C . cos ( A B C ; α ) ^ = 1 2
Chú ý lý thuyết: Nếu đa giác (H) trong mặt phẳng (P) có diện tích S, đa giác (H) trong mặt phẳng là hình chiếu vuông góc (H) của có diện tích S', φ là góc giữa (P), (P') thì S ' = S . cos φ

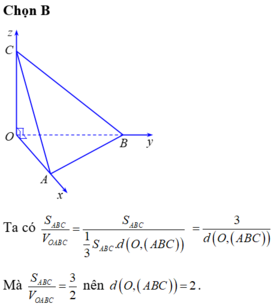
Vậy mặt phẳng (ABC) luôn tiếp xúc mặt cầu tâm O, bán kính R = 2.

Đáp án C
Phương pháp:
+) Gọi A(0;0;a) (a>0) viết phương trình đường thẳng AB đi qua A và vuông góc với ( α )
![]()
tìm tọa độ điểm B theo a
+) Tam giác MAB cân tại M => MA = MB, tìm a.
+) Sử dụng công thức tính diện tích
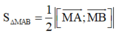
Cách giải:
![]()
=> Phương trình đường thẳng
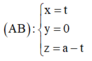
![]()
![]()
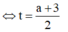
Khi đó
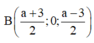
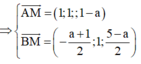
![]()
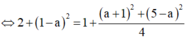
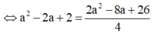
![]()
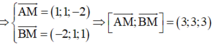
Vậy diện tích tam giác MAB là
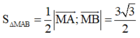

Chọn B
Gọi A (0; 0; a). Đường thẳng AB qua A và vuông góc với (α) có phương trình 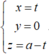
B là hình chiếu của A lên (α) nên tọa độ B thỏa mãn hệ
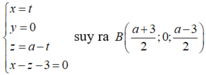
Tam giác MAB cân tại M nên
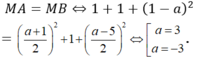
· Nếu a = -3 thì tọa độ A (0; 0; -3) và B (0; 0; -3) trùng nhau, loại.
· Nếu a = 3 thì tọa độ A (0; 0; 3), B (3; 0; 0)
Diện tích tam giác MAB bằng
![]()

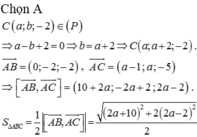
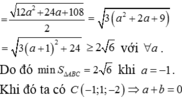

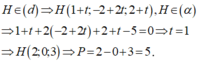

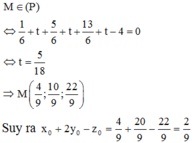
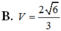

Đáp án B