Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{xy\left(z-1\right)-y\left(z-1\right)-x\left(z-1\right)+\left(z-1\right)}{xy\left(z+1\right)+y\left(z+1\right)-x\left(z+1\right)-\left(z+1\right)}\\ =\dfrac{\left(z-1\right)\left(xy-y-x+1\right)}{\left(z+1\right)\left(xy+y-x-1\right)}=\dfrac{\left(z-1\right)\left(x-1\right)\left(y-1\right)}{\left(z+1\right)\left(x+1\right)\left(y-1\right)}=\dfrac{\left(z-1\right)\left(x-1\right)}{\left(z+1\right)\left(x+1\right)}\\ =\dfrac{\left(5003-1\right)\left(5001-1\right)}{\left(5003+1\right)\left(5001+1\right)}=\dfrac{5002\cdot5000}{5004\cdot5002}=\dfrac{5000}{5004}=\dfrac{1250}{1251}\)

?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????


\(A=\dfrac{x}{xy+x+1}+\dfrac{xy}{x.yz+xy+x}+\dfrac{xy.z}{xy.xz+xy.z+xy}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{1+xy+x}+\dfrac{1}{x+1+xy}\)
\(=\dfrac{x+xy+1}{xy+x+1}=1\)

cũng dễ thôi
M=\(\dfrac{1}{1+x+xy}+\dfrac{1}{1+y+yz}+\dfrac{1}{1+z+zx}\)
\(M=\dfrac{z}{z\left(1+x+xy\right)}+\dfrac{xz}{xz\left(1+y+yz\right)}+\dfrac{xyz}{xyz\left(1+z+zx\right)}\\ =\dfrac{z}{z+xz+xyz}+\dfrac{xz}{xz+xyz+xyz\left(z\right)}+\dfrac{xyz}{xyz+xyz\left(z\right)+xyz\left(xz\right)}\\ màxyz=1\\ nênM=\dfrac{z}{z+xz+1}+\dfrac{xz}{z+xz+1}+\dfrac{1}{z+xz+1}\\ vậyM=\dfrac{z+xz+1}{z+xz+1}=1\)
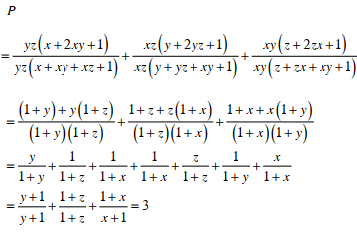
Hồi lớp 8 mk làm bài này hoài:
Ta có: \(\dfrac{x}{xy+x+1}+\dfrac{y}{yz+y+1}+\dfrac{z}{zx+z+1}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{xyz+xy+x}+\dfrac{xyz}{x^2yz+xyz+xy}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{xy+x+1}+\dfrac{1}{xy+x+1}\) ( vì \(xyz=1\) )
\(=\dfrac{x+xy+1}{xy+x+1}\)
\(=1\)
Hok tốt!