Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{xy+x+xyz}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{xyz}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz}{y+1+yz}+\dfrac{1}{y+yz+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+1}{y+1+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+xyz}{y+xyz+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{y\left(z+xz\right)}{y\left(1+xz+z\right)}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{z+xz+1}{xz+z+1}\)
\(A=1\)

?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

\(M=\dfrac{x}{x+xy+1}+\dfrac{xy}{xyz+xy+x}+\dfrac{z}{xz+z+xyz}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{xy+x+1}+\dfrac{z}{\left(xy+x+1\right)z}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{xy+x+1}+\dfrac{1}{xy+x+1}=1\)

Các thánh giúp e nha Ace Legona Nguyễn Huy Tú Toshiro Kiyoshi Phương An Akai Haruma @Nguyễn Vũ Phượng Thảo

\(A=\dfrac{x^3+y^3+z^3}{xyz}=\dfrac{\left(x+y\right)^3+z^3-3xy\left(x+y\right)}{xyz}\)
\(=\dfrac{\left(-z\right)^3+z^3-3xy\left(-z\right)}{xyz}=3\)

\(A=\dfrac{xyz.x}{xy+xyz.x+xyz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{xyz+yz+y}\)
\(=\dfrac{xz}{1+xz+z}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{xyz}{y+xyz+yz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{2019}{y+2019+yz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{yz+y+2019}{yz+y+2019}=1\)

\(x,y,z\ne0\)
-Ta c/m: -Với \(a+b+c=0\) thì: \(a^3+b^3+c^3-3abc=0\)
\(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0.\left(a^2+b^2+c^2-ab-bc-ca\right)=0\left(đpcm\right)\)
-Quay lại bài toán:
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\Rightarrow\dfrac{xy+yz+zx}{xyz}=0\Rightarrow xy+yz+zx=0\)
\(A=\dfrac{yz}{x^2}+\dfrac{zx}{y^2}+\dfrac{xy}{z^2}=\dfrac{y^3z^3+z^3x^3+x^3y^3}{x^2y^2z^2}=\dfrac{y^3z^3+z^3x^3+x^3y^3-3x^2y^2z^2+3x^2y^2z^2}{x^2y^2z^2}=\dfrac{\left(xy+yz+zx\right)\left[x^2y^2+y^2z^2+z^2x^2-xyz\left(x+y+z\right)\right]}{x^2y^2z^2}+3=\dfrac{0.\left[x^2y^2+y^2z^2+z^2x^2-xyz\left(x+y+z\right)\right]}{x^2y^2z^2}+3=3\)

\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2yz+2xz=x^2+y^2+z^2+2\left(xy+yz+xz\right)\)
\(\Rightarrow2\left(xy+yz+xz\right)=\left(x+y+z\right)^2+\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2\left(xy+yz+xz\right)=a^2+b\)
\(\Rightarrow xy+yz+xz=\dfrac{a^2+b}{2}\)
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{c}\Rightarrow\dfrac{xy+yz+xz}{xyz}=\dfrac{1}{c}\)
\(\Rightarrow xyz=c\left(xy+yz+xz\right)\)
\(\Rightarrow xyz=\dfrac{\left(a^2+b\right)c}{2}\)
\(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
\(\Rightarrow x^3+y^3+z^3=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)+3xyz\)
\(\Rightarrow x^3+y^3+z^3=\left(x+y+z\right)\left(x^2+y^2+z^2-\left(xy+yz+xz\right)\right)+3xyz\)
\(\Rightarrow x^3+y^3+z^3=a\left(b-\dfrac{a^2+b}{2}\right)+3\dfrac{\left(a^2+b\right)c}{2}\)
\(\Rightarrow x^3+y^3+z^3=a\dfrac{\left(b-a^2\right)}{2}+3\dfrac{\left(a^2+b\right)c}{2}\)
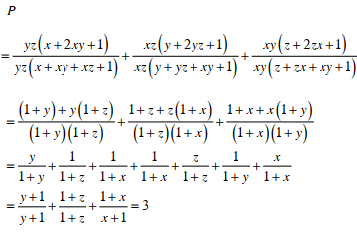
\(A=\dfrac{x}{xy+x+1}+\dfrac{xy}{x.yz+xy+x}+\dfrac{xy.z}{xy.xz+xy.z+xy}\)
\(=\dfrac{x}{xy+x+1}+\dfrac{xy}{1+xy+x}+\dfrac{1}{x+1+xy}\)
\(=\dfrac{x+xy+1}{xy+x+1}=1\)