Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.

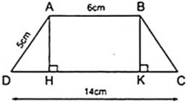
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: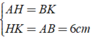
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
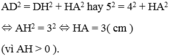
Vậy chiều cao của hình thang cân là 3cm.

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

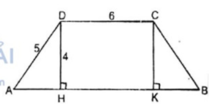
Xét hình thang cân ABCD có AB // CD
Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm
Đường cao DH = 4cm. Kẻ CK ⊥ AB
Ta có tứ giác CDHK là hình chữ nhật
HK = CD = 6cm
△ AHD vuông tại H. Theo định lý Pi-ta-go ta có: A D 2 = A H 2 + D H 2
⇒ A H 2 = A D 2 - D H 2 = 5 2 - 4 2 = 25 – 16 = 9 ⇒ AH = 3cm
Xét hai tam giác vuông DHA và CKB :
∠ (DHA)= ∠ (CKB)= 90 0
AD = BC (tính chất hình thang cân)
∠ A = ∠ B(gt)
Do đó: △ DHA = △ CKB (cạnh huyền, góc nhọn)
⇒ KB = AH = 3 (cm)
AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)
S A B C D = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( c m 2 )


Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)


Kẻ 2 đường cao AH và BH'
Xét hai tam giác vuông AHD và BH'C ,có :
AD = BC ( gt )
\(\widehat{D}\)=\(\widehat{C}\) ( gt )
=> tam giác AHD = tam giác BH'C ( ch - gn )
=> HD = H'C ( hai cạnh tương ứng )
Kẻ AH'
Xét tam giác ABH' và tam giác H'HA , có :
AH' : chung
góc B = góc C ( = 90o ) - AB//DC
H'B = AH ( tam giác AHD = tam giác BH'C )
=> tam giác ABH' = tam giác H'HA ( ch - cgv )
=> AB = H'H ( hai cạnh tương ứng ) => HH' = 6cm
Ta lại có : DH + HH' + H'C = 14cm
=> DH + HH' = 8cm => DH = 4cm
Xét tam giác AHD vuông tại H
=> AD2 = AH2 + HD2 ( định lý Py - ta - go )
=> 52 = AH2 + 42
=> 25 = AH2 + 16
=> AH2 = 9
=> AH = 3 hoặc AH = -3 mà AH > 0 => AH = 3cm
Vậy ...( đpcm )