Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

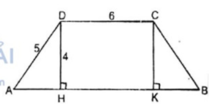
Xét hình thang cân ABCD có AB // CD
Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm
Đường cao DH = 4cm. Kẻ CK ⊥ AB
Ta có tứ giác CDHK là hình chữ nhật
HK = CD = 6cm
△ AHD vuông tại H. Theo định lý Pi-ta-go ta có: A D 2 = A H 2 + D H 2
⇒ A H 2 = A D 2 - D H 2 = 5 2 - 4 2 = 25 – 16 = 9 ⇒ AH = 3cm
Xét hai tam giác vuông DHA và CKB :
∠ (DHA)= ∠ (CKB)= 90 0
AD = BC (tính chất hình thang cân)
∠ A = ∠ B(gt)
Do đó: △ DHA = △ CKB (cạnh huyền, góc nhọn)
⇒ KB = AH = 3 (cm)
AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)
S A B C D = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( c m 2 )


1) a) Do ABCD là hình thang cân => góc D = góc C ; góc B = góc A
Trong t/g ABC có : góc A = 90 độ => góc D + góc C2 = 90 độ
Trong t/g ABC có AB = BC ( gt ) => t/g ABC cân tại B => góc A1 = góc C1
Ta có góc A = 90 độ + góc A1 = góc D + góc C2 + góc C1 = góc C + góc C = 2C
Mà :
A + B + C + D = 360 độ = 2A + 2C = 4C + 2C = 6C => góc C = 360 độ : 6 = 60 độ
=> góc C = góc D ( = 60 độ ) ; góc A = góc B ( = 120 độ )

Đáp án cần chọn là: B

Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có D ^ = C ^ ; AD = BC
=> ΔAHD = ΔBKC (ch – gn) => DH = CK
Suy ra DH = 1 2 (CD – AB)
Suy ra DH = 1 2 (CD – AB) = 1 2 (10 – 4)
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
A D 2 = A H 2 + D H 2 ⇒ A H 2 = A D 2 - D H 2 = 5 2 - 3 2 ⇒ A H = 4
Vậy AH = 4cm.

1. Tính được AH=3cm theo định lý Pitago, vẽ đường cao CK (K thuộc AB), tính được BK=3cm nên HK=6cm nên AB=12cm, lúc đó sẽ tinhd được diện tích hình thang
2. Tương tự