TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BN
1
4 tháng 4 2020
Bg
Ta có: \(\frac{a}{b}=\frac{36}{45}\)và ƯCLN (a, b) = 31
=> \(\frac{a}{b}=\frac{4}{5}\)
=> a = 31m; b = 31n (m, n \(\inℕ^∗\); m và n nguyên tố cùng nhau)
=> \(\frac{31m}{31n}=\frac{4}{5}\)
=> \(\frac{m}{n}=\frac{4}{5}\)
Vì m và n nguyên tố cùng nhau nên m = 4 và n = 5.
=> \(\frac{31m}{31n}=\frac{31.4}{31.5}=\frac{124}{155}\)
=> \(\frac{a}{b}=\frac{124}{155}\)
Vậy...
VT
2
20 tháng 4 2020
\(\frac{a}{b}=\frac{36}{45}=\frac{4}{5}\)
(a,b) = 31 chứng tỏ phân số \(\frac{a}{b}\)rút gọn cho 31 được \(\frac{4}{5}\)
Vậy \(\frac{a}{b}=\frac{4.31}{5.31}=\frac{124}{155}\)
20 tháng 4 2020
phân số\(\frac{a}{b}\)tối giản là \(\frac{4}{5}\)
vì ƯCLN (a;b) = 31\(\Rightarrow\)a;b \(\in\)B(31)={31;62;96;124;155;...}
mà 124=31.4; 155=31.5\(\Rightarrow\)\(\frac{a}{b}\)=\(\frac{124}{155}\)
PT
1
PT
1
5 tháng 6 2016
a) Phân số đó có dạng
9k20k
Ta có BCNN(9k; 20k) = 360
Mà BCNN(9; 20) = 180
Do đó k = 360 : 180 = 2
=> 9k = 9 . 2 = 18 và 20k = 20 . 2 = 40
Phân số phải tìm là \(\frac{18}{40}\)
5 tháng 6 2016
Vì ƯCLN(20,39)=36 nên số lần giản ước của 20/39 là 36
Vậy PS cần tìm: 20.36/39.36=720/1404
MT
0
SN
2
SG
11 tháng 2 2018
Đáp án câu hỏi trên là :20/36. Đúng 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
30 tháng 12 2021
a,Vì ƯCLN(a,b)=15 nên \(\Rightarrow\) \(\hept{\begin{cases}a=15m\\b=15n\end{cases}}\) với ƯCLN (m,n) = 1
Vì \(\frac{a}{b}\)=\(\frac{60}{108}\) nên \(\frac{15m}{15n}\) =\(\frac{60}{108}\) \(\Leftrightarrow\)\(\hept{\begin{cases}m=5\\n=9\end{cases}\Rightarrow\hept{\begin{cases}a=15.5=75\\b=15.9=135\end{cases}}}\)
Vậy phân số \(\frac{a}{b}=\frac{75}{135}\)
phần b làm tương tự nha nhớ k nhá
TV
1
14 tháng 2 2015
Vi 20/9 la phan so toi gian nen phan so can tim co dang 20k/9k.
Vi UCLN(20k,9k)=36
=> UCLN(20,9).k=36
1.k =36
=> k=36
Vậy phân số cần tìm là 720/324.
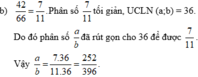
Phân số a và b phải bằng phân số 36 phần 45 và ước bằng 31
\(\Rightarrow\frac{a}{b}=\frac{36\cdot31}{45\cdot31}=\frac{1116}{1395}\)
Đáp số:\(\frac{1116}{1395}\)