K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 7 2017
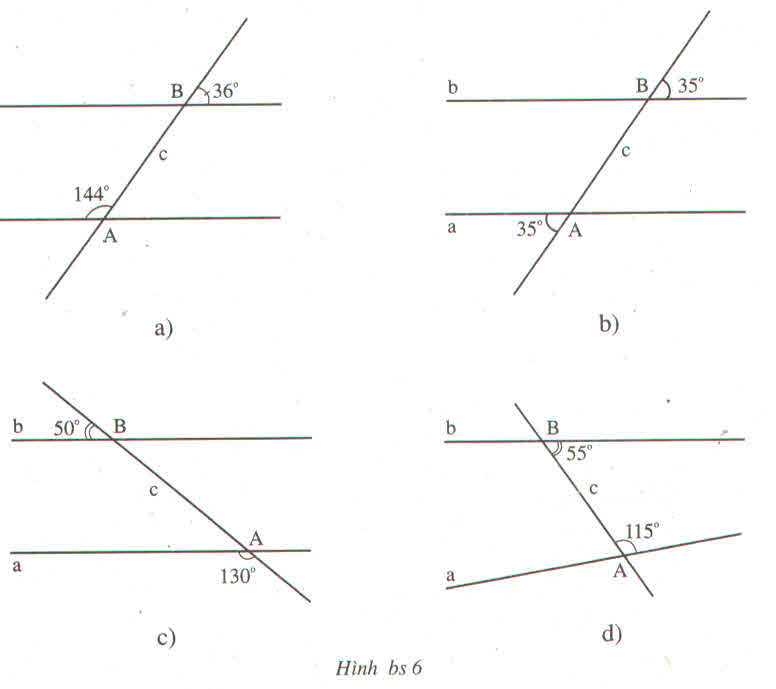
Trong trường hợp hình d) thì a và b không song song với nhau vì tổng hai góc trong cùng phía không bằng \(180^0\)
6 tháng 7 2017
trong hình a) ta có : 180 - 36 =144 (vì 2 góc bù nhau )
vậy a song song b (vì 2 góc đồng vị bằng nhau)
trong hình b) ta có : a song song b (vì 2 so le ngoài bằng nhau )
trong hình c) ta có : 180 - 50 =130 (vì 2 góc bù nhau )
vậy a song song b (vì 2 góc đồng vị bằng nhau )
trong hình d) a không song song với b ( vì hai góc trong cùng phía không bù nhau )
LT
12 tháng 5 2017
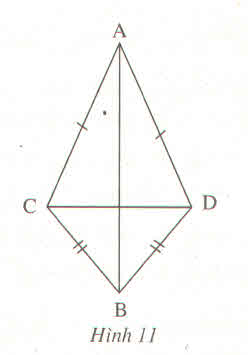
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD
TM
2 tháng 10 2017
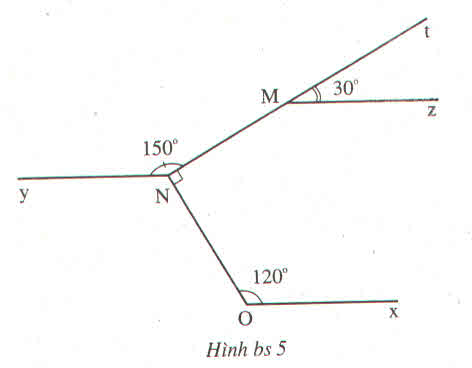
a) Vì góc tMz và góc NMz kề bù nên:
\(\widehat{tMz}+\widehat{NMz}=180^o\)
\(\Rightarrow30^o+\widehat{NMz}=180^o\)
\(\Rightarrow\widehat{NMz}=180^o-30^o=150^o\)
Ta có: \(\widehat{NMz}=\widehat{MNy}=150^o\)
\(\Rightarrow\) Mz // Ny (vì có cặp góc so le trong bằng nhau)
16 tháng 6 2017
a) 2 đường thẳng Mz và Ny song song
b) 2 đường thẳng Ny và Ox không song song vì 2 góc so le trong không bằng nhau
SG
3
QD
20 tháng 4 2017
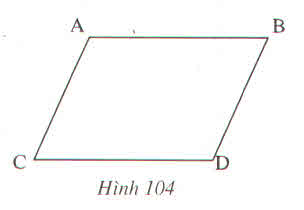
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
ˆA1A1^= ˆD1D1^(so le trong AB//CD)
AD là cạnh chung.
A2^=D2^(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
Xem thêm tại: http://loigiaihay.com/bai-38-trang-124-sach-giao-khoa-toan-7-tap-1-c42a5073.html#ixzz4elm8F0eT
6 tháng 8 2017
A B C D
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
\(\widehat{A^1}\)= \(\widehat{D^1}\)(so le trong AB//CD)
AD là cạnh chung.
\(\widehat{A^2}\)=\(\widehat{D^2}\)(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
18 tháng 5 2022
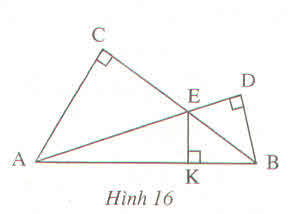
Xét ΔAEB có
AC là đường cao
BD là đường cao
EK là đường cao
Do đó: AC,BD,EK cùng đi qua một điểm
SG
2
QD
20 tháng 4 2017
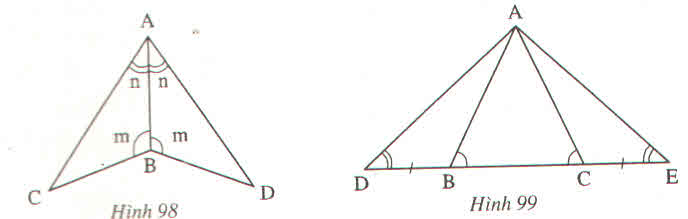
- Xem hình 98
∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
- Xem hình 99.
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)
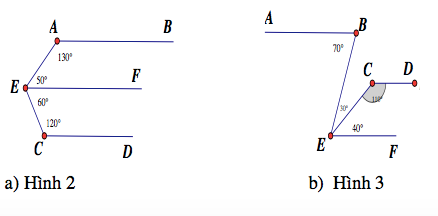
\(a,\widehat{BAE}+\widehat{AEF}=180^0\\ \text{Mà 2 góc này ở vị trí TCP nên AB//EF(1)}\\ \widehat{FEC}+\widehat{ECD}=180^0\\ \text{Mà 2 góc này ở vị trí TCP nên EF//CD(2)}\\ \left(1\right)\left(2\right)\Rightarrow AB//CD\)
\(b,\widehat{BEF}=\widehat{BEC}+\widehat{CEF}=70^0=\widehat{ABE}\\ \text{Mà 2 góc này ở vị trí so le trong nên AB//EF(1)}\\ \widehat{CEF}+\widehat{ECD}=180^0\\ \text{Mà 2 góc này ở vị trí TCP nên EF//CD(2)}\\ \left(1\right)\left(2\right)\Rightarrow AB//CD\)