Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
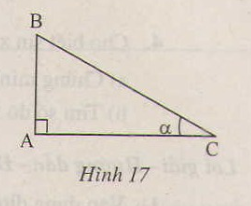
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
sin60° = cos(90° – 60°) = cos30°
Tương tự:
cos75° = sin(90° – 75°) = sin 15°
sin52°30′ = cos(90° – 52°30′) = 38°30′
cotg82° = tg8°; tg80° = cotg10°

tớ mới tham gia nên k biết viết anpha,tớ sẽ viết là @ nhé.hình vẽ là tam giác ABC có Bc và cạnh huyền,AB là cạnh kề còn AC là cạnh đối(tớ cho góc B làm góc anpha)
a,tan@=AC/AB
sin@=AC/BC (1),cos@=AB/BC (2)
từ (1) và (2) suy ra sin@/cos@=AC/BC : AB/BC = AC/BC x BC/AB= AC/AB
mà tan@ = AC/AB
=>tan@=sin@/cos@
những câu sau làm tương tự nhé

a) sin a=0,8
Ta có: \(\sin^2a+\cos^2a=1\)
\(\Rightarrow\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\orbr{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
\(\sin a=0,8\)
\(\sin^2a=1-\sin^2a=1\)
\(\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\hept{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
Code : Breacker

Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)

\(\sin60^o=\cos30^o\)
\(\cos75^o=\sin15^o\)
\(\cot82^o=\tan8^o\)
\(\tan80^o=\cot10^o\)
\(\sin52^o3'=\cos37^o57'\)
\(sin60=cos\left(90^0-60^0\right)=cos30^0\)
\(cos75^0=sin\left(90^0-75^0\right)=sin15^0\)
\(cot82^0=tan\left(90^0-82^0\right)=tan8^0\)
\(tan80^0=cot\left(90^0-80^0\right)=cot10^0\)
\(sin52^03'=cos\left(90^0-52^03'\right)=cos37^057'\)

\(sin57^0=cos\left(90^0-57^0\right)=cos33^0\)
\(cos43^032'\) ko cần biến đổi vì góc đã thỏa mãn
\(tan72^015'=cot\left(90^0-72^015'\right)=cot\left(17^045'\right)\)
\(cot\left(85^035'\right)=tan\left(90^0-85^035'\right)=tan\left(4^025'\right)\)
Vì 75 ° + 15 ° = 90 ° nên sin 75 ° = cos 15 °
Vì 53 ° + 37 ° = 90 ° nên cos 53 ° = sin 37 °
Vì 47 ° 20 ' + 42 ° 40 ' = 90 ° nên sin 47 ° 20 ' = cos 42 ° 40 '
Vì 62 ° + 28 ° = 90 ° nên tg 62 ° = cotg 28 °
Vì 82 ° 45 ' + 7 ° 15 ' = 90 ° nên cotg 82 ° 45 ' = tg 7 ° 15 '