
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sin a=12/13
cos^2a=1-(12/13)^2=25/169
=>cosa=5/13
tan a=12/13:5/13=12/5
cot a=1:12/5=5/12
sin b=căn 3/2
cos^2b=1-(căn 3/2)^2=1/4
=>cos b=1/2
tan b=căn 3/2:1/2=căn 3
cot b=1/căn 3

Hướng dẫn giải:
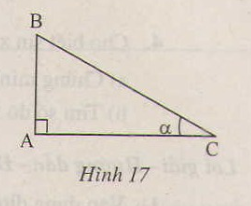
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
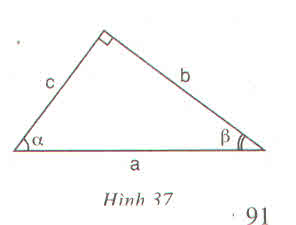
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.



a, Theo hệ thức lượng trong tam giác vuông AMB ta có
\(cos\alpha=\frac{MA}{AB}\Leftrightarrow MA=2a.cos\alpha\)
\(sin\alpha=\frac{MB}{AB}\Rightarrow MB=2a.sin\alpha\)
Vì \(\hept{\begin{cases}MH\perp d\\AB\perp d\end{cases}\Rightarrow MH//AB}\)
=> MH=KB
mà \(KB=AB-AK=2a-MA.cos\alpha=2a-2a.cos^2\alpha\)


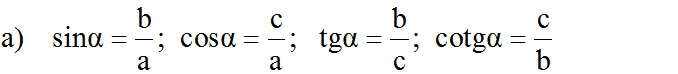
a) sin a=0,8
Ta có: \(\sin^2a+\cos^2a=1\)
\(\Rightarrow\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\orbr{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
\(\sin a=0,8\)
\(\sin^2a=1-\sin^2a=1\)
\(\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\hept{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
Code : Breacker